题目内容
(08年宣武区质量检一文)(14分)
已知二次函数f(x)=![]() 同时满足:
同时满足:![]() ①不等式f(x)
①不等式f(x)![]() 0的解集有且只有一个元素②在定义域内存在0
0的解集有且只有一个元素②在定义域内存在0![]() ,使得不等式
,使得不等式![]() 成立。设数列{
成立。设数列{![]() }的前n项和
}的前n项和![]() .
.
(1) 求函数f(x)的表达式;
(2) 求数列{![]() }的通项公式;
}的通项公式;
设各项均不为零的数列{![]() }中,所有满足
}中,所有满足![]() 的整数i的个数称为这个数列{
的整数i的个数称为这个数列{![]() }的变号数。令
}的变号数。令![]() (n为正整数),求数列{
(n为正整数),求数列{![]() }的变号数。
}的变号数。
解析:(1)![]() f(x)
f(x)![]() 0的解集有且只有一个元素,
0的解集有且只有一个元素,
![]()
![]() 或a=4
或a=4
当a=4时,函数![]() 在(0,2)上递减
在(0,2)上递减
故存在![]() 使不等式
使不等式![]() 成立
成立
当a=0时,函数![]() 在(0,
在(0,![]() )上递增
)上递增
故不存在![]() ,使不等式
,使不等式![]() 成立
成立
综上,得a=4,![]() ………………5分
………………5分
(2)由(1)可知
当n=1时,![]() ,
,
当n![]() 时,
时,![]()
![]() ………………9分
………………9分
(3)由题设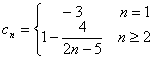
![]() n
n![]() 时,
时,![]()
![]() n
n![]() 时,数列{
时,数列{![]() }递增。
}递增。
因为![]() ,由1
,由1![]() 得n
得n![]() ,可知
,可知
![]() ,即n
,即n![]() 时,有且只有1个变号数。
时,有且只有1个变号数。
又因为![]() ,即
,即![]()
综上得数列{![]() }的变号数为3………………14分
}的变号数为3………………14分

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目

