题目内容
已知实数组成的数组(x1,x2,x3,…,xn)满足条件:①
xi=0; ②
|xi|=1.
(1)当n=2时,求x1,x2的值;
(2)当n=3时,求证:|3x1+2x2+x3|≤1;
(3)设a1≥a2≥a3≥…≥an,且a1>an(n≥2),求证:|
aixi|≤
(a1-an).
| n |
 |
| i=1 |
| n |
 |
| i=1 |
(1)当n=2时,求x1,x2的值;
(2)当n=3时,求证:|3x1+2x2+x3|≤1;
(3)设a1≥a2≥a3≥…≥an,且a1>an(n≥2),求证:|
| n |
 |
| i=1 |
| 1 |
| 2 |
分析:(1)当n=2时,通过已知条件列出方程组,然后求x1,x2的值;
(2)当n=3时,利用条件列出x1+x2+x3=0,|x1|+|x2|+|x3|=1,通过|3x1+2x2+x3|=|x1+2(x1+x2+x3)-x3|,
然后证明|3x1+2x2+x3|≤1;
(3)通过a1≥ai≥an,且a1>an(i=1,2,3,…,n).转化为|(a1-ai)-(ai-an)|≤|(a1-ai)+(ai-an)|=|a1-an|,推出|a1+an-2ai|≤|a1-an|,借助(2)的证明方法证明:|
aixi|≤
(a1-an).
(2)当n=3时,利用条件列出x1+x2+x3=0,|x1|+|x2|+|x3|=1,通过|3x1+2x2+x3|=|x1+2(x1+x2+x3)-x3|,
然后证明|3x1+2x2+x3|≤1;
(3)通过a1≥ai≥an,且a1>an(i=1,2,3,…,n).转化为|(a1-ai)-(ai-an)|≤|(a1-ai)+(ai-an)|=|a1-an|,推出|a1+an-2ai|≤|a1-an|,借助(2)的证明方法证明:|
| n |
 |
| i=1 |
| 1 |
| 2 |
解答:解:(1)解:
由(1)得x2=-x1,再由(2)知x1≠0,且x2≠0.
当x1>0时,x2<0.得2x1=1,所以
…(2分)
当x1<0时,同理得
…(4分)
(2)证明:当n=3时,
由已知x1+x2+x3=0,|x1|+|x2|+|x3|=1.
所以|3x1+2x2+x3|=|x1+2(x1+x2+x3)-x3|=|x1-x3|≤|x1|+|x3|≤1.…(9分)
(3)证明:因为a1≥ai≥an,且a1>an(i=1,2,3,…,n).
所以|(a1-ai)-(ai-an)|≤|(a1-ai)+(ai-an)|=|a1-an|,
即|a1+an-2ai|≤|a1-an|(i=1,2,3,…,n).…(11分)
|
aixi|=|
aixi-
a1
xi-
an
xi|
=
|
(2ai-a1-an)xi|
≤
(|a1+an-2ai||xi|)
≤
(|a1-an||xi|)
=
|a1-an|
|xi|
=
(a1-an).…(14分)
|
由(1)得x2=-x1,再由(2)知x1≠0,且x2≠0.
当x1>0时,x2<0.得2x1=1,所以
|
当x1<0时,同理得
|
(2)证明:当n=3时,
由已知x1+x2+x3=0,|x1|+|x2|+|x3|=1.
所以|3x1+2x2+x3|=|x1+2(x1+x2+x3)-x3|=|x1-x3|≤|x1|+|x3|≤1.…(9分)
(3)证明:因为a1≥ai≥an,且a1>an(i=1,2,3,…,n).
所以|(a1-ai)-(ai-an)|≤|(a1-ai)+(ai-an)|=|a1-an|,
即|a1+an-2ai|≤|a1-an|(i=1,2,3,…,n).…(11分)
|
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| 1 |
| 2 |
| n |
 |
| i=1 |
| 1 |
| 2 |
| n |
 |
| i=1 |
=
| 1 |
| 2 |
| n |
 |
| i=1 |
≤
| 1 |
| 2 |
| n |
 |
| i=1 |
≤
| 1 |
| 2 |
| n |
 |
| i=1 |
=
| 1 |
| 2 |
| n |
 |
| i=1 |
=
| 1 |
| 2 |
点评:本题考查含绝对值不等式的证明,方程组的求法,注意求和表达式的应用,考查转化思想与计算能力.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
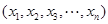 满足条件:
满足条件: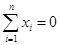 ; ②
; ②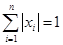 .
.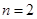 时,求
时,求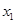 ,
,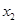 的值;
的值;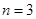 时,求证:
时,求证: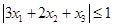 ;
;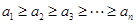 ,且
,且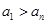
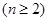 ,求证:
,求证: .
.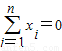 ; ②
; ② .
.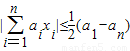 .
.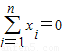 ; ②
; ② .
. .
.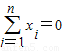 ; ②
; ②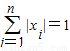 .
.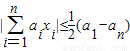 .
.