题目内容
6.在锐角三角形ABC,角A.B,C的对边分别为a,b,c,满足向量$\overrightarrow{m}$=(2a-c,b),向量$\overrightarrow{n}$=(cosC,cosB),且$\overrightarrow{m}$∥$\overrightarrow{n}$.求t=$\frac{c}{a}$时t的取值范围.分析 利用向量共线的坐标表示求得B,结合三角形为锐角三角形求得A的范围,然后把t=$\frac{c}{a}$转化为含有A的正切得答案.
解答 解:由$\overrightarrow{m}$=(2a-c,b),向量$\overrightarrow{n}$=(cosC,cosB),且$\overrightarrow{m}$∥$\overrightarrow{n}$,
得(2a-c)cosB-bcosC=0,
结合正弦定理得:(2sinA-sinC)cosB-sinBcosC=0,
整理得:cosB=$\frac{1}{2}$,∴B=60°.
∵△ABC为锐角三角形,则0°<A<90°,且0°<120°-A<90°,得30°<A<90°.
∴tanA$>\frac{\sqrt{3}}{3}$,
则t=$\frac{c}{a}$=$\frac{sinC}{sinA}$=$\frac{sin(120°-A)}{sinA}$=$\frac{\frac{\sqrt{3}}{2}cosA+\frac{1}{2}sinA}{sinA}$=$\frac{\frac{\sqrt{3}}{2}+\frac{1}{2}tanA}{tanA}$=$\frac{1}{2}+\frac{\sqrt{3}}{2tanA}$∈($\frac{1}{2},2$).
点评 本题考查了平面向量的坐标运算,考查了三角函数值域的求法,是中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
2.焦点在x轴上的椭圆$\frac{x^2}{m}+\frac{y^2}{3}=1$的离心率是$\frac{1}{2}$,则实数m的值是( )
| A. | 4 | B. | $\frac{9}{4}$ | C. | 1 | D. | $\frac{3}{4}$ |
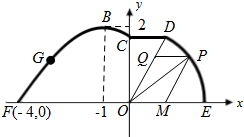 如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+ϕ)(A>0,ω>0,
如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+ϕ)(A>0,ω>0, 在四棱锥P-ABCD中,PA⊥底面ABCD,PA=1,底面ABCD是正方形,E是PD的中点,PD与底面ABCD所成的角为$\frac{π}{6}$,求异面直线AE与PC 所成的角的大小.
在四棱锥P-ABCD中,PA⊥底面ABCD,PA=1,底面ABCD是正方形,E是PD的中点,PD与底面ABCD所成的角为$\frac{π}{6}$,求异面直线AE与PC 所成的角的大小.