Question

如图2-5-3所示，已知ABCD是菱形，AC和BD是它的两条对角线.

求证：AC⊥BD.

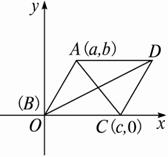
图2-5-3

Answer 1

证法一：∵,，

∴·=()·()=||²-||²=0.

∴⊥,即AC⊥BD.

证法二：以BC所在直线为x轴，以B为原点建立直角坐标系，设B(0，0)，A(a，b)，C(c，0)，则由|AB|=|BC|得a²+b²=c².

∵=(c，0)-(a，b)=(c-a，-b)，

=(a，b)+(c，0)=(c+a，b)，

∴·BD=c²-a²-b²=0.

∴⊥，即AC⊥BD.