题目内容
已知函数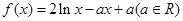 .
.
(Ⅰ)讨论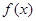 的单调性;
的单调性;
(Ⅱ)若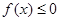 恒成立,证明:当
恒成立,证明:当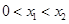 时,
时,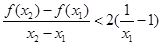 .
.
【答案】
(Ⅰ)当 时,
时, 在
在 上递增;当
上递增;当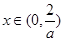 时,
时, 单调递增;当
单调递增;当 时,
时, 单调递减;(Ⅱ)证明过程详见解析.
单调递减;(Ⅱ)证明过程详见解析.
【解析】
试题分析:本题主要考查导数的运算,利用导数研究函数的单调区间、最值等数学知识和方法,突出考查分类讨论思想和综合分析问题和解决问题的能力.第一问是利用导数研究函数的单调性,但是题中有参数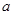 ,需对参数
,需对参数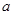 进行讨论,可以转化为含参一元一次不等式的解法;第二问先是恒成立问题,通过第一问的单调性对
进行讨论,可以转化为含参一元一次不等式的解法;第二问先是恒成立问题,通过第一问的单调性对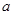 进行讨论,通过求函数的最大值求出符合题意的
进行讨论,通过求函数的最大值求出符合题意的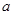 ,表达式确定后,再利用函数的单调性的定义,作差,放缩法证明不等式.
,表达式确定后,再利用函数的单调性的定义,作差,放缩法证明不等式.
试题解析:(Ⅰ)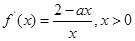 .
.
若 ,
,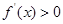 ,
, 在
在 上递增;
上递增;
若 ,当
,当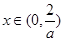 时,
时,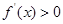 ,
, 单调递增;
单调递增;
当 时,
时, ,
, 单调递减.
5分
单调递减.
5分
(Ⅱ)由(Ⅰ)知,若 ,
, 在
在 上递增,
上递增,
又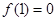 ,故
,故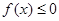 不恒成立.
不恒成立.
若 ,当
,当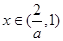 时,
时, 递减,
递减, ,不合题意.
,不合题意.
若 ,当
,当 时,
时, 递增,
递增, ,不合题意.
,不合题意.
若 ,
, 在
在 上递增,在
上递增,在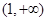 上递减,
上递减,
 符合题意,
符合题意,
故 ,且
,且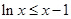 (当且仅当
(当且仅当 时取“
时取“ ”). 8分
”). 8分
当 时,
时,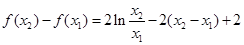
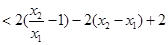
 ,
,
所以 . 12分
. 12分
考点:1.利用导数求函数的单调性;2.恒成立问题;3.分类讨论思想和放缩法的应用.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
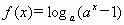 ,(
,(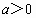 ,
,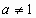 ),
),
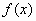 的定义域;
的定义域;
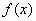 的单调性.
的单调性.