题目内容
(本小题满分12分)
设函数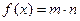 ,其中向量
,其中向量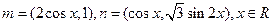 .
.
(1) 求函数
求函数 的最
的最 小正周期与单调递减区间;
小正周期与单调递减区间;
(2)在△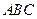 中,
中,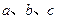 分别是角
分别是角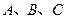
 的对边,已知
的对边,已知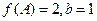 ,△
,△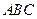 的面积为
的面积为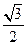 ,求△
,求△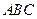 外接圆半径
外接圆半径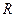 .
.
设函数
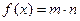 ,其中向量
,其中向量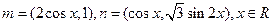 .
.(1)
 求函数
求函数 的最
的最 小正周期与单调递减区间;
小正周期与单调递减区间;(2)在△
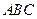 中,
中,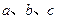 分别是角
分别是角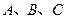
 的对边,已知
的对边,已知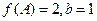 ,△
,△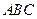 的面积为
的面积为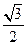 ,求△
,求△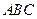 外接圆半径
外接圆半径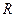 .
.(1)
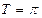 ,
,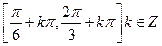 (2)1
(2)1

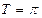 ,
,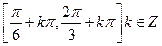 (2)1
(2)1(1)由题意得
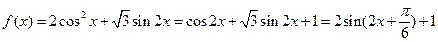 .
.
所以,函数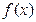 的最小正周期为
的最小正周期为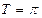 ,由
,由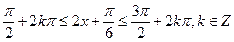 得
得
 函数
函数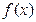 的单调递减区间是
的单调递减区间是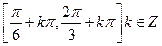 ……………………………6分
……………………………6分
(2)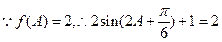 ,解得
,解得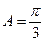 ,
,
又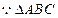 的面积为
的面积为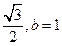 。得
。得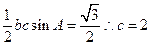 。
。
再由余弦定理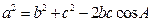 ,解得
,解得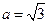

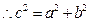 ,即△
,即△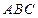 为直角三角形.
为直角三角形. …………………………l2分
…………………………l2分
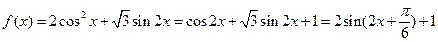 .
.所以,函数
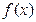 的最小正周期为
的最小正周期为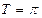 ,由
,由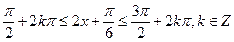 得
得 函数
函数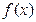 的单调递减区间是
的单调递减区间是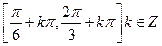 ……………………………6分
……………………………6分(2)
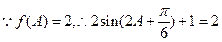 ,解得
,解得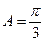 ,
,又
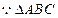 的面积为
的面积为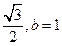 。得
。得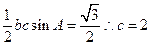 。
。再由余弦定理
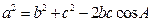 ,解得
,解得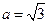

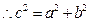 ,即△
,即△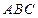 为直角三角形.
为直角三角形. …………………………l2分
…………………………l2分
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
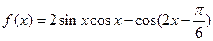 .
.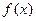 的最小正周期;
的最小正周期;
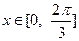 时,求函数
时,求函数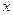 的值.
的值. 的值为 ( )
的值为 ( )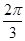
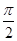

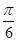
 的最大值是( )
的最大值是( )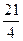
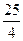

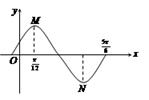
 在一个周期内的图象,
在一个周期内的图象,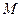 、
、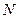 分别是最大、最小值点,且
分别是最大、最小值点,且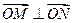 ,则
,则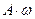 的值为( )
的值为( )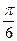
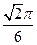

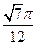
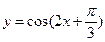 的图象,只要将
的图象,只要将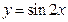 的图象
的图象 个单位
个单位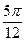 个单位
个单位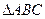 中,若
中,若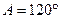 ,AB=5,AC=4,则
,AB=5,AC=4,则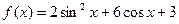 的最大值为
的最大值为