题目内容
若圆C过点M(0,1)且与直线l:y=-1相切,设圆心C的轨迹为曲线E,A、B为曲线E上的两点,点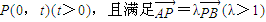 .
.(I)求曲线E的方程;
(II)若t=6,直线AB的斜率为
 ,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;(III)分别过A、B作曲线E的切线,两条切线交于点Q,若点Q恰好在直线l上,求证:t与
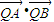 均为定值.
均为定值.
【答案】分析:(1)由点C到定点M的距离等于到定直线l的距离与抛物线的定义可得点C的轨迹为抛物线所以曲线E的方程为x2=4y.
(2)由题得直线AB的方程是x-2y+12=0联立抛物线的方程解得A(6,9)和B(-4,4),进而直线NA的方程为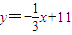 ,由A,B两点的坐标得到线段AB中垂线方程为
,由A,B两点的坐标得到线段AB中垂线方程为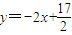 ,可求N点的坐标,进而求出圆N的方程
,可求N点的坐标,进而求出圆N的方程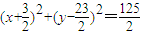 .
.
(3)设A,B两点的坐标,由题意得过点A的切线方程为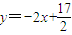 又Q(a,-1),可得x12-2ax1-4=0同理得x22-2ax2-4=0所以x1+x2=2a,x1x2=-4.所以直线AB的方程为
又Q(a,-1),可得x12-2ax1-4=0同理得x22-2ax2-4=0所以x1+x2=2a,x1x2=-4.所以直线AB的方程为
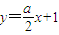 所以t=-1.根据向量的运算得
所以t=-1.根据向量的运算得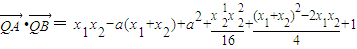 =0.
=0.
解答:【解】(Ⅰ)依题意,点C到定点M的距离等于到定直线l的距离,所以点C的轨迹为抛物线,曲线E的方程为x2=4y.
(Ⅱ)直线AB的方程是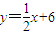 ,即x-2y+12=0.
,即x-2y+12=0.
由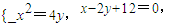 及
及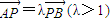 知
知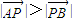 ,得A(6,9)和B(-4,4)
,得A(6,9)和B(-4,4)
由x2=4y得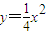 ,
,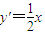 .
.
所以抛物线x2=4y在点A处切线的斜率为y'|x=6=3.
直线NA的方程为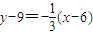 ,即
,即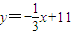 .①
.①
线段AB的中点坐标为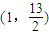 ,线段AB中垂线方程为
,线段AB中垂线方程为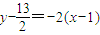 ,即
,即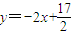 .②
.②
由①、②解得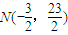 .
.
于是,圆C的方程为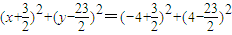 ,
,
即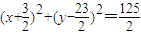 .
.
(Ⅲ)设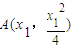 ,
,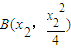 ,Q(a,-1).过点A的切线方程为
,Q(a,-1).过点A的切线方程为 ,
,
即x12-2ax1-4=0.同理可得x22-2ax2-4=0,所以x1+x2=2a,x1x2=-4.
又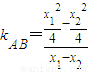 =
= ,所以直线AB的方程为
,所以直线AB的方程为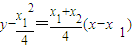 ,
,
即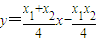 ,亦即
,亦即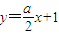 ,所以t=-1.
,所以t=-1.
而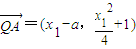 ,
,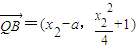 ,
,
所以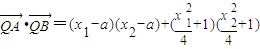
=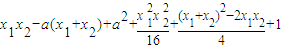
=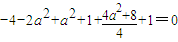 .
.
点评:本题主要考查抛物线的定义和直线与曲线的相切问题,解决此类问题的必须熟悉曲线的定义和曲线的图形特征,这也是高考常考的知识点.
(2)由题得直线AB的方程是x-2y+12=0联立抛物线的方程解得A(6,9)和B(-4,4),进而直线NA的方程为
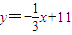 ,由A,B两点的坐标得到线段AB中垂线方程为
,由A,B两点的坐标得到线段AB中垂线方程为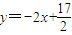 ,可求N点的坐标,进而求出圆N的方程
,可求N点的坐标,进而求出圆N的方程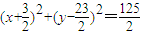 .
.(3)设A,B两点的坐标,由题意得过点A的切线方程为
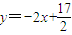 又Q(a,-1),可得x12-2ax1-4=0同理得x22-2ax2-4=0所以x1+x2=2a,x1x2=-4.所以直线AB的方程为
又Q(a,-1),可得x12-2ax1-4=0同理得x22-2ax2-4=0所以x1+x2=2a,x1x2=-4.所以直线AB的方程为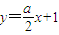 所以t=-1.根据向量的运算得
所以t=-1.根据向量的运算得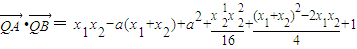 =0.
=0.解答:【解】(Ⅰ)依题意,点C到定点M的距离等于到定直线l的距离,所以点C的轨迹为抛物线,曲线E的方程为x2=4y.
(Ⅱ)直线AB的方程是
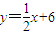 ,即x-2y+12=0.
,即x-2y+12=0.由
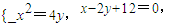 及
及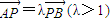 知
知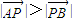 ,得A(6,9)和B(-4,4)
,得A(6,9)和B(-4,4)由x2=4y得
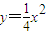 ,
,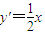 .
.所以抛物线x2=4y在点A处切线的斜率为y'|x=6=3.
直线NA的方程为
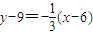 ,即
,即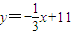 .①
.①线段AB的中点坐标为
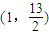 ,线段AB中垂线方程为
,线段AB中垂线方程为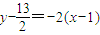 ,即
,即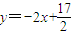 .②
.②由①、②解得
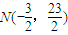 .
.于是,圆C的方程为
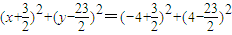 ,
,即
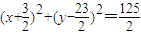 .
.(Ⅲ)设
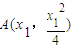 ,
,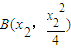 ,Q(a,-1).过点A的切线方程为
,Q(a,-1).过点A的切线方程为 ,
,即x12-2ax1-4=0.同理可得x22-2ax2-4=0,所以x1+x2=2a,x1x2=-4.
又
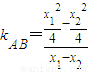 =
= ,所以直线AB的方程为
,所以直线AB的方程为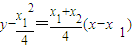 ,
,即
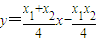 ,亦即
,亦即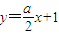 ,所以t=-1.
,所以t=-1.而
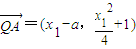 ,
,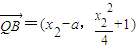 ,
,所以
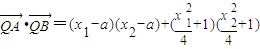
=
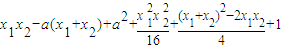
=
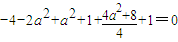 .
.点评:本题主要考查抛物线的定义和直线与曲线的相切问题,解决此类问题的必须熟悉曲线的定义和曲线的图形特征,这也是高考常考的知识点.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
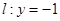 相切,设圆心C的轨迹为曲线E,A、B(A在y轴的右侧)为曲线E上的两点,点
相切,设圆心C的轨迹为曲线E,A、B(A在y轴的右侧)为曲线E上的两点,点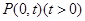 ,且满足
,且满足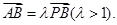
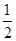 ,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;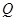 ,若点
,若点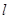 上,求证:t与
上,求证:t与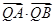 均为定值.
均为定值.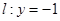 相切,设圆心C的轨迹为曲线E,A、B为曲线E上的两点,点
相切,设圆心C的轨迹为曲线E,A、B为曲线E上的两点,点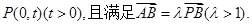
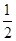 ,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;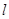 上,求证:t与
上,求证:t与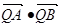 均为定值。
均为定值。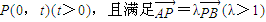 .
. ,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;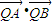 均为定值.
均为定值.