题目内容
（09年雅礼中学月考文）（13分）已知椭圆
中心在坐标原点，焦点在坐标轴上，且经过
、
、
三点．过椭圆的右焦点F任做一与坐标轴不平行的直线
与椭圆交于
、
两点，
与
所在的直线交于点Q.
（1）求椭圆的方程：
（2）是否存在这样直线
，使得点Q恒在直线上移动？若存在,求出直线方程,若不存在,请说明理由.
解析：（1）设椭圆方程为
-------------------------（1分）
将
、
、
代入椭圆E的方程，得
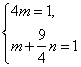解得
.------------------------------------（4分）
∴椭圆
的方程
--------------------------------------- （5分）
（也可设标准方程，知
类似计分）
（2） 可知：将直线
----------------------------------------（6分）
代入椭圆的方程并整理．得
----（7分）
设直线
与椭圆的交点
，
由根系数的关系，得
---------------------（8分）
直线
的方程为：
由直线的方程为：
，即
-------------（9分）
由直线与直线
的方程消去
，得
---------------------（10分）
---------------（12分）
与直线的交点在直线
上． 故这样的直线存在-----------（13分） 
练习册系列答案
智能训练练测考系列答案
相关题目
；若仅通过面试而笔试不通过，则被确认为通过自主招生的可能性为
；两者均不通过，则淘汰。现知有一报考该校自主招生的学生在推荐材料审核，笔试，面试这三环节中通过的概率分别为
，假设各环节之间互不影响.试求：
的首项和公比均为
．
（
）各项的和；
，求这个子数列的通项公式；
是椭圆
的顶点（如图）,直线
与椭圆交于异于顶点的
两点,且
．若椭圆的离心率是
,且
．
和直线
的倾斜角分别
．试判断
是否为定值？若是，求出此定值；若不是，说明理由． 
（
），就得到奖金
元，且答对题
（
元，
，
元，
时，某人选择先回答题1，设获得奖金为
，求
．
，
，若答题人无论先回答哪个问题，答题人可能得到的奖金一样多，求此时
的值．