题目内容
(12分)学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏中,①摸出3个白球的概率;②获奖的概率;(6分)
(2)求在2次游戏中获奖次数X的分布列及数学期望E(X). (6分)
【答案】
(1)①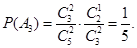 ;
②
;
②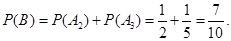 ;
;
(2)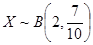 ,
,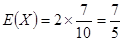
【解析】①求出基本事件总数,计算摸出3个白球事件数,利用古典概型公式,代入数据得到结果;②获奖包含摸出2个白球和摸出3个白球,且它们互斥,根据①求出摸出2个白球的概率,再相加即可求得结果;
(2)确定在2次游戏中获奖次数X的取值是0、1、2,求出相应的概率,即可写出分布列,求出数学期望.
解:(1)①设“在1次游戏中摸出i个白球”为事件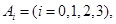
则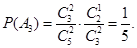 …………………2分
…………………2分
②设“在1次游戏中获奖”为事件B,则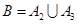 ,A2,A3互斥,
,A2,A3互斥,
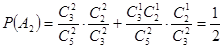 …………………4分
…………………4分
所以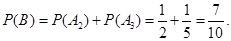 …………………6分
…………………6分
(2)法Ⅰ解:由题意可知X的所有可能取值为0,1,2. ……………7分
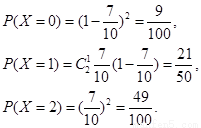
……………………………………………10分
所以X的分布列是
|
X |
0 |
1 |
2 |
|
P |
|
|
|
X的数学期望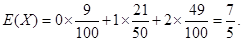 ……………12分
……………12分
法Ⅱ: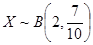 ,于是可依次得
,于是可依次得
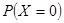 ,
,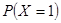 ,
,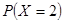 ;
;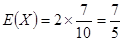

练习册系列答案
相关题目
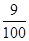
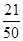
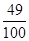
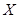 的分布列及数学期望
的分布列及数学期望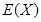 .
.