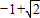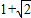Question

连接抛物线x²=4y的焦点F与点M（1，0）所得的线段与抛物线交于点A，设点O为坐标原点，则三角形OAM的面积为（　　）

• A、-1+

  2

• B、

  3

  2

  -

  2

• C、1+

  2

• D、

  3

  2

  +

  2

Answer 1

分析：先求出直线FM的方程，然后与抛物线方程联立方程组解得点A的纵坐标，最后利用三角形面积公式求解．

解答：解：抛物线x²=4y的焦点F为（0，1）且M（1，0），
所以直线FM所在的直线方程为x+y=1，
与抛物线方程联立有

x+y=1 x2=4y

，
解得y₁=3-2

2

，y₂=3+2

2

，
因为点A是线段FM与抛物线x²=4y的交点，所以点A的纵坐标为3-2

2

，
所以S△OAM=

1

2

× 1×(3-2

2

)=

3

2

-

2

．
故选B．

点评：本题主要考查代数法研究形，同时考查抛物线焦点坐标、直线方程等知识点．