题目内容
设△ABC顶点坐标A(0,1),B(-
,0),C(
,0),圆M为△ABC的外接圆.
(Ⅰ)求圆M的标准方程;
(Ⅱ)直线l过点(1,3)且与圆M相交于P、Q,弦PQ长为2
,求直线l的方程.
| 3 |
| 3 |
(Ⅰ)求圆M的标准方程;
(Ⅱ)直线l过点(1,3)且与圆M相交于P、Q,弦PQ长为2
| 3 |
分析:(Ⅰ)设圆M的一般方程为x2+y2+Dx+Ey+F=0,将点A(0,1),B(-
,0),C(
,0)代入可得方程组,由此可得圆M的标准方程;
(Ⅱ)若直线l与x轴垂直,则l:x=1,可知符合题意;若直线l与x轴不垂直,设l:y=k(x-1)+3即kx-y-k+3=0,求得点M(0,-1)到l的距离d=
,利用弦PQ长为2
,即可求得直线l的方程.
| 3 |
| 3 |
(Ⅱ)若直线l与x轴垂直,则l:x=1,可知符合题意;若直线l与x轴不垂直,设l:y=k(x-1)+3即kx-y-k+3=0,求得点M(0,-1)到l的距离d=
| |4-k| | ||
|
| 3 |
解答:解:(Ⅰ)设圆M的方程为x2+y2+Dx+Ey+F=0
因为圆M过点A(0,1),B(-
,0),C(
,0),所以
,…(4分)
解得
,所以圆M的方程为x2+y2+2y-3=0,即x2+(y+1)2=4. (7分)
(Ⅱ)若直线l与x轴垂直,则l:x=1,
由
,得
,所以PQ=2
,符合题意. …(9分)
若直线l与x轴不垂直,设l:y=k(x-1)+3即kx-y-k+3=0
点M(0,-1)到l的距离d=
∴PQ=2
=2
=2
,…(12分)
∴k=
,此时l方程为y=
x+
综上所述,直线l的方程是x=1或y=
x+
. …(15分)
因为圆M过点A(0,1),B(-
| 3 |
| 3 |
|
解得
|
(Ⅱ)若直线l与x轴垂直,则l:x=1,
由
|
|
| 3 |
若直线l与x轴不垂直,设l:y=k(x-1)+3即kx-y-k+3=0
点M(0,-1)到l的距离d=
| |4-k| | ||
|
∴PQ=2
| r2-d2 |
4-
|
| 3 |
∴k=
| 15 |
| 8 |
| 15 |
| 8 |
| 7 |
| 8 |
综上所述,直线l的方程是x=1或y=
| 15 |
| 8 |
| 7 |
| 8 |
点评:本题考查圆的标准方程,考查直线与圆相交的弦长问题,解题的关键是利用待定系数法,利用圆的特殊性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,直角三角形ABC的顶点坐标A(-1,0),直角顶点
如图,直角三角形ABC的顶点坐标A(-1,0),直角顶点 如图,直角三角形ABC的顶点坐标A(-1,0),直角顶点
如图,直角三角形ABC的顶点坐标A(-1,0),直角顶点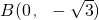 ,顶点C在x轴上.
,顶点C在x轴上.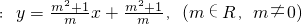 ,直线?能否与圆M相交?为什么?若能相交,直线?能否将圆M分割成弧长的比值为
,直线?能否与圆M相交?为什么?若能相交,直线?能否将圆M分割成弧长的比值为 的两段弧?为什么?
的两段弧?为什么? ,顶点C在x轴上.
,顶点C在x轴上. ,直线?能否与圆M相交?为什么?若能相交,直线?能否将圆M分割成弧长的比值为
,直线?能否与圆M相交?为什么?若能相交,直线?能否将圆M分割成弧长的比值为 的两段弧?为什么?
的两段弧?为什么?