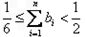题目内容
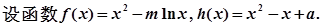
(1)当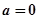 时,
时,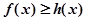 在
在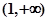 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(2)当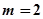 时,若函数
时,若函数 在
在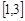 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数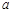 的取值范围;
的取值范围;
(3)是否存在实数 ,使函数f(x)和函数
,使函数f(x)和函数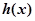 在公共定义域上具有相同的单调区间?若存在,求出
在公共定义域上具有相同的单调区间?若存在,求出 的值,若不存在,说明理由。
的值,若不存在,说明理由。
解:(1)由a=0,f(x)≥h(x)可得-mlnx≥-x,即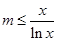
记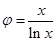 ,则f(x)≥h(x)在(1,+∞)上恒成立等价于
,则f(x)≥h(x)在(1,+∞)上恒成立等价于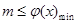 .求得
.求得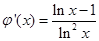
当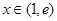 时;
时;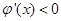 ;当
;当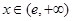 时,
时,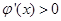
故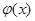 在x=e处取得极小值,也是最小值,
在x=e处取得极小值,也是最小值,
即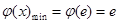 ,故
,故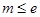 .
.
(2)函数k(x)=f(x)-h(x)在[1,3]上恰有两个不同的零点等价于方程x-2lnx=a,在[1,3]上恰有两个相异实根。
令g(x)=x-2lnx,则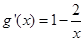
当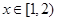 时,
时,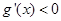 ,当
,当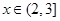 时,
时,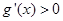
g(x)在[1,2]上是单调递减函数,在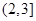 上是单调递增函数。
上是单调递增函数。
故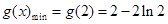
又g(1)=1,g(3)=3-2ln3
∵g(1)>g(3),∴只需g(2)<a≤g(3),
故a的取值范围是(2-2ln2,3-2ln3]
(3)存在m=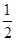 ,使得函数f(x)和函数h(x)在公共定义域上具有相同的单调性
,使得函数f(x)和函数h(x)在公共定义域上具有相同的单调性
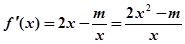 ,函数f(x)的定义域为(0,+∞)。
,函数f(x)的定义域为(0,+∞)。
若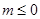 ,则
,则 ,函数f(x)在(0,+∞)上单调递增,不合题意;
,函数f(x)在(0,+∞)上单调递增,不合题意;
若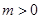 ,由
,由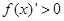 可得2x2-m>0,解得x>
可得2x2-m>0,解得x>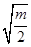 或x<-
或x<-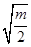 (舍去)
(舍去)
故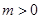 时,函数的单调递增区间为(
时,函数的单调递增区间为(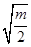 ,+∞), 单调递减区间为(0,
,+∞), 单调递减区间为(0, 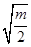 )
)
而h(x)在(0,+∞)上的单调递减区间是(0,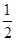 ),单调递增区间是(
),单调递增区间是(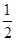 ,+∞)
,+∞)
故只需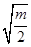 =
=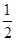 ,解之得m=
,解之得m=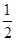
即当m=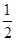 时,函数f(x)和函数h(x)在其公共定义域上具有相同的单调性
时,函数f(x)和函数h(x)在其公共定义域上具有相同的单调性
【解析】略

己知在锐角ΔABC中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]()
(I )求角![]() 大小;
大小;
(II)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

20.如图1,在平面内,![]() 是
是![]() 的矩形,
的矩形,![]() 是正三角形,将
是正三角形,将![]() 沿
沿![]() 折起,使
折起,使![]() 如图2,
如图2,![]() 为
为![]() 的中点,设直线
的中点,设直线![]() 过点
过点![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,点
所在平面,点![]() 是直线
是直线![]() 上的一个动点,且与点
上的一个动点,且与点![]() 位于平面
位于平面![]() 的同侧。
的同侧。
(1)求证:![]() 平面
平面![]() ;
;
(2)设二面角![]() 的平面角为
的平面角为![]() ,若
,若![]() ,求线段
,求线段![]() 长的取值范围。
长的取值范围。


21.已知A,B是椭圆![]() 的左,右顶点,
的左,右顶点,![]() ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线![]() 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
(1)求椭圆C的方程;
 (2)求三角形MNT的面积的最大值
(2)求三角形MNT的面积的最大值
22. 已知函数![]()
![]() ,
,
(Ⅰ)若![]() 在
在![]() 上存在最大值与最小值,且其最大值与最小值的和为
上存在最大值与最小值,且其最大值与最小值的和为![]() ,试求
,试求![]() 和
和![]() 的值。
的值。
(Ⅱ)若![]() 为奇函数:
为奇函数:
(1)是否存在实数![]() ,使得
,使得![]() 在
在![]() 为增函数,
为增函数,![]() 为减函数,若存在,求出
为减函数,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)如果当![]() 时,都有
时,都有![]() 恒成立,试求
恒成立,试求![]() 的取值范围.
的取值范围.
(理)如图,平面ADEF⊥平面ABCD,ABCD与ADEF均为矩形,且AB:AD:AF=
|
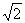 :2:
:2: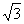 ;P为线段EF上一点,M为AB的中点,若PC与BD所成的角为
;P为线段EF上一点,M为AB的中点,若PC与BD所成的角为
60°.
(1)试确定P点位置;
(2)求二面角P—MC—D的大小的余弦值;
(3)当AB长为多少时,点D到平面PMC的距离等于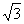 ?
?
(文)设函数 (
( ),其中
),其中 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求函数
时,求函数 的极大值和极小值;
的极大值和极小值;
(Ⅲ)当 时,证明存在
时,证明存在 ,使得不等式
,使得不等式 对任意的
对任意的 恒成立.
恒成立.
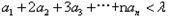 (
(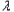 ∈R)恒成立时,求
∈R)恒成立时,求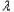 的最小值;
的最小值;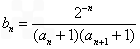 时,求证:
时,求证: