Question

如图是求

1

1×2

+

1

2×3

+

1

3×4

+…+

1

99×100

的算法的程序框图．
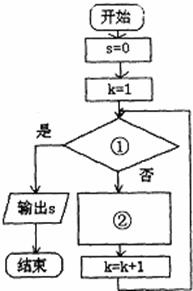
（1）标号①处填______，标号②处填______．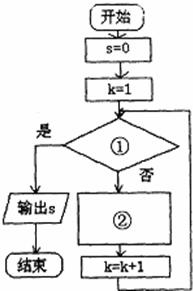

Answer 1

k=1，满足条件①，执行循环体，S=

1

1×2

k=2，满足条件①，执行循环体，S=

1

1×2

+

1

2×3

依此类推
k=98，满足条件①，执行循环体，S=

1

1×2

+

1

2×3

+…

1

9×10

k=99，不满足条件①，退出循环体，输出S=

1

1×2

+

1

2×3

+

1

3×4

+…+

1

99×100

，
所以当k=1，2，3…99满足判断框的条件，当k=100不满足判断框的条件
所以判断框①中的条件是k＞99，
标号②处作用是求和，故填S=S+

1

k(k+1)

故答案为：k＞99；S=S+

1

k(k+1)