题目内容
长方体AC1中,底面ABCD为边长为2的正方形,高AA1为1,M、N分别是边C1D1与A1D1的中点.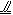
(1)求证:四边形MNAC是等腰梯形;
(2)求梯形MNAC的面积.
思路解析:(1)要证明一个四边形是等腰梯形,应证明①四边形是平面图形;②有一组对边平行;③另一组对边不相等.
(2)只需利用(1)的结论,并利用梯形的面积公式,即要得出问题的解答.
解:(1)连结A1C1,则MN是△A1C1D1的中位线,于是MN![]()
![]() A1C1
A1C1
又A1C1![]() AC,
AC,
∴MN![]()
![]() AC.
AC.
∴M、N、A、C共面,且四边形MNAC为梯形.
∵Rt△AA1N≌Rt△CC1M,
∴AN=CM.
∴梯形MNAC为等腰梯形.
(2)AN2=A1A2+A1N2=1+1=2,AC=2![]() ,MN=
,MN=![]() ,
,
梯形的高为h=![]()
∴S梯形ACMN=![]() (AC+MN)×h=
(AC+MN)×h=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

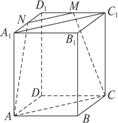
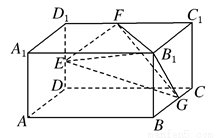
 平面
平面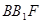 ;
;