题目内容
若a>3,则函数f(x)=x2-ax+1在区间(0,2)上恰好有 个零点
【答案】
1;
【解析】
试题分析:也a>3,则函数f(x)=x2-ax+1图象开口向上,过点(0,1),对称轴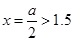 ,f(2)=5-2a<0,所以,恰有1个零点。
,f(2)=5-2a<0,所以,恰有1个零点。
考点:本题主要考查二次函数的零点。
点评:简单题,本题给定了区间及对称轴范围,因此,应注意讨论图象的特征及函数的单调性。

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目