题目内容
已知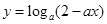 在
在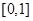 上是
上是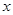 的减函数,则
的减函数,则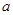 的取值范围是( )
的取值范围是( )
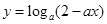 在
在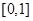 上是
上是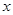 的减函数,则
的减函数,则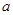 的取值范围是( )
的取值范围是( )A. | B. | C.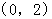 | D. |
B
试题分析:原函数是由简单函数t=2-ax和y=logat共同复合而成.
∵a>0,∴t=2-ax为定义域上减函数,
而由复合函数法则和题意得到,
y=logat在定义域上为增函数,∴a>1
又函数t=2-ax>0在(0,1)上恒成立,则2-a<0即可.
∴a<2.综上,1<a<2,
故答案为B
点评:解决该试题的关键是解决对数函数问题时,注意真数位置的范围.本题中如若不注意这一点,会导致答案错误的为(1,+∞).这也是考生的易错点.

练习册系列答案
相关题目
 ,则满足不等式
,则满足不等式 的x的范围是( )
的x的范围是( )

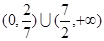

 是( )
是( ) 上单调递增
上单调递增 上单调递增
上单调递增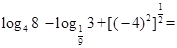 _____________.
_____________.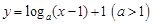 的图象必过定点( )
的图象必过定点( )
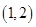


 在[0,1]上是
在[0,1]上是 的减函数,则
的减函数,则 的取值范围是( )
的取值范围是( ) )
)
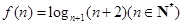 ,定义:使
,定义:使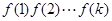 为整数的数
为整数的数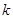
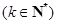 叫作企盼数,则在区间
叫作企盼数,则在区间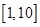 内这样的企盼数共有 个.
内这样的企盼数共有 个.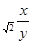 的值( )
的值( )