题目内容
已知函数![]() .
.
(Ⅰ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,是否存在过点(1,-1)的直线与函数
时,是否存在过点(1,-1)的直线与函数![]() 的图象相切?若存在,有多少条?若不存在,说明理由.
的图象相切?若存在,有多少条?若不存在,说明理由.
解析:(1)由题意![]() .
.
当![]() 时,函数
时,函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,则
,则![]() ,
,![]() ,则
,则![]() ,
,
此时函数在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
当![]() 时,函数
时,函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,则
,则![]() ,
,![]() ,则
,则![]() ,
,
此时函数在![]() 上是减函数,在
上是减函数,在![]() 上是增函数。
上是增函数。
(2)假设存在这样的切线,设其中一个切点![]() ,
,
∴切线方程:![]() ,将点
,将点![]() 坐标代入得:
坐标代入得:
![]() ,即
,即![]() , ①
, ①
设![]() ,则
,则![]() .
.
令![]() ,则
,则![]() 或
或![]() 。
。
|
| (0,1) | 1 | (1,2) | 2 |
|
|
| + | 0 | - | 0 | + |
|
| 递增 | 极大值 | 递减 | 极小值 |
|
所以![]() 在区间
在区间![]() ,
,![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数,
上是减函数,
![]() 在
在![]() 处取得极大值
处取得极大值![]() ,在
,在![]() 处取得极小值
处取得极小值![]() ,
,
所以![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上无解。
上无解。
因为![]() ,
,![]() ,
,![]() 在区间
在区间![]() 上单调递增,根据零点定理,
上单调递增,根据零点定理,![]() 在区间
在区间![]() 上有且仅有一个实数根,即方程①有且仅有一解,故符合条件的切线有且仅有一条.
上有且仅有一个实数根,即方程①有且仅有一解,故符合条件的切线有且仅有一条.

练习册系列答案
相关题目
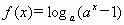 ,(
,(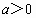 ,
,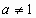 ),
),
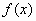 的定义域;
的定义域;
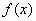 的单调性.
的单调性.