题目内容
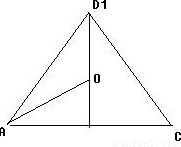
如图,已知球O是棱长为1的正方体ABCB-A1B1C1D1的内切球,则平面ACD1截球O的截面面积为( )

(A)
 (B)
(B) (C)
(C)  ( D)
( D)

【答案】
A
【解析】
试题分析:根据正方体的几何特征知,平面ACD1是边长为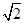 的正三角形,且球与与以点D为公共点的三个面的切点恰为三角形ACD1三边的中点,
的正三角形,且球与与以点D为公共点的三个面的切点恰为三角形ACD1三边的中点,
故所求截面的面积是该正三角形的内切圆的面积,
则由图得,△ACD1内切圆的半径是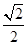 ×tan30°=
×tan30°=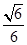 ,
,
则所求的截面圆的面积是π×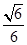 ×
×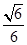 =
=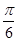 ,
,
故选A.
考点:正方体及其内接球的几何特征
点评:中档题,关键是想象出截面图的形状,利用转化与化归思想,将空间问题转化成平面问题。

练习册系列答案
相关题目
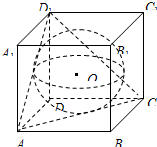 如图,已知球O是棱长为1的正方体ABCD-A1B1C1D1的内切球,则平面ACD1截球O的截面面积为( )
如图,已知球O是棱长为1的正方体ABCD-A1B1C1D1的内切球,则平面ACD1截球O的截面面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 (2012•桂林模拟)如图,已知球O是棱长为1 的正方体ABCD-A1B1C1D1的内切球,则平面ACD1截球o的截面面积为
(2012•桂林模拟)如图,已知球O是棱长为1 的正方体ABCD-A1B1C1D1的内切球,则平面ACD1截球o的截面面积为 的内切球,则平面
的内切球,则平面 截球O的截面面积为
.
截球O的截面面积为
.