题目内容
如图,P是双曲线 上的动点,F1、F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且
上的动点,F1、F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且 .某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2M的中点,得
.某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2M的中点,得 .类似地:P是椭圆
.类似地:P是椭圆 上的动点,F1、F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且
上的动点,F1、F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且 .则|OM|的取值范围是 .
.则|OM|的取值范围是 .
【答案】分析:椭圆与双曲线都是平面上到定点和定直线距离之比为定值的动点的轨迹,故他们的研究方法、性质都是相似之处,我们由题目中根据双曲线的性质,探究|OM|值方法,类比椭圆的性质,推断出椭圆中|OM|的取值范围.
解答:解:延长F2M交PF1于点N,可知△PNF2为等腰三角形,
且M为F2M的中点,
则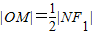 =a-|F2M|
=a-|F2M|
∵a-c<|F2M|<a
故0<|OM|<c=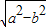
故|OM|的取值范围是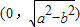
故答案为: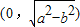
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).
解答:解:延长F2M交PF1于点N,可知△PNF2为等腰三角形,
且M为F2M的中点,
则
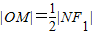 =a-|F2M|
=a-|F2M|∵a-c<|F2M|<a
故0<|OM|<c=
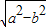
故|OM|的取值范围是
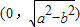
故答案为:
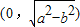
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
.如图,P是双曲线 上的动点,F1、
上的动点,F1、
F2是双曲线的焦点,M是 的平分线上一点,且
的平分线上一点,且
某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知 为
为
等腰三角形,且M为F2M的中点,得
|
 上的动点,F1、F2是椭圆的焦点,M是
上的动点,F1、F2是椭圆的焦点,M是 的平分线上一点,且
的平分线上一点,且 .则|OM|的取值范围是
.则|OM|的取值范围是

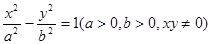 上的动点,
上的动点, 、
、 是双曲线的左右焦点,
是双曲线的左右焦点, 是
是 的平分线上一点,且
的平分线上一点,且 某同学用以下方法研究
某同学用以下方法研究 :延长
:延长 交
交 于点
于点 ,可知
,可知 为等腰三角形,且M为
为等腰三角形,且M为 的中点,得
的中点,得 类似地:P是椭圆
类似地:P是椭圆 上的动点,
上的动点, ,则
,则
 上的动点,F1、F2是双曲线的焦点,M是
上的动点,F1、F2是双曲线的焦点,M是 的平分线上一点,且
的平分线上一点,且 某同学用以下方法研究|OM|:延长
某同学用以下方法研究|OM|:延长 交
交 于点N,可知
于点N,可知 为等腰三角形,且M为
为等腰三角形,且M为 的中点,得
的中点,得 类似地:P是椭圆
类似地:P是椭圆 上的动点,F1、F2是椭圆的焦点,M是
上的动点,F1、F2是椭圆的焦点,M是 ,则|OM|的取值范围是
.
,则|OM|的取值范围是
.
 上的动点,F1、F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且
上的动点,F1、F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且 .某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2M的中点,得
.某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2M的中点,得 .类似地:P是椭圆
.类似地:P是椭圆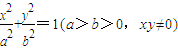 上的动点,F1、F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且
上的动点,F1、F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且 .则|OM|的取值范围是 .
.则|OM|的取值范围是 .