题目内容
某学校课题小组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
(1)根据上表完成下面的2×2列联表(单位:人):
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | |||
| 物理成绩不优秀 | |||
| 合计 | 20 |
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率.
参考数据:
①假设有两个分类变量X和Y,它们的值域分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:
| y1 | y2 | 合计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 合计 | a+c | b+d | a+b+c+d |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
②独立检验随机变量K2的临界值参考表:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析:(1)由“单科成绩85分以上(含85分),则该科成绩为优秀”.及已知中高二年级20名学生某次考试成绩,我们易得到列联表的各项数据.
(2)我们可以根据列联表中的数据,代入公式K2=
,计算出k值,然后代入离散系数表,比较即可得到答案.
(3)本小题考查的知识点是古典概型,关键是要找出满足条件抽到的学生数学成绩与物理成绩至少有一门不优秀的基本事件个数,及总的基本事件的个数,再代入古典概型公式进行计算求解.
(2)我们可以根据列联表中的数据,代入公式K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
(3)本小题考查的知识点是古典概型,关键是要找出满足条件抽到的学生数学成绩与物理成绩至少有一门不优秀的基本事件个数,及总的基本事件的个数,再代入古典概型公式进行计算求解.
解答:(1)解:2×2列联表为(单位:人):
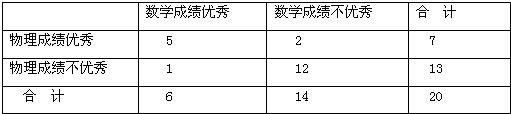
(2)解:提出假设H0:学生数学成绩与物理成绩之间没有关系.
根据列联表可以求得K2=
≈8.802>7.879.
当H0成立时,P(K2>7.879)=0.005.
所以我们有99.5%的把握认为:学生的数学成绩与物理成绩之间有关系.
(3)解:由(1)可知数学成绩与物理成绩都优秀的学生的人数为5人,
则数学成绩与物理成绩至少有一门不优秀的学生人数为15人.
故从20名学生中抽出1名,抽到的学生数学成绩与物理成绩至少有一门不优秀的概率为
=
.

(2)解:提出假设H0:学生数学成绩与物理成绩之间没有关系.
根据列联表可以求得K2=
| 20×(5×12-1×2)2 |
| 6×14×7×13 |
当H0成立时,P(K2>7.879)=0.005.
所以我们有99.5%的把握认为:学生的数学成绩与物理成绩之间有关系.
(3)解:由(1)可知数学成绩与物理成绩都优秀的学生的人数为5人,
则数学成绩与物理成绩至少有一门不优秀的学生人数为15人.
故从20名学生中抽出1名,抽到的学生数学成绩与物理成绩至少有一门不优秀的概率为
| 15 |
| 20 |
| 3 |
| 4 |
点评:本小题主要考查独立性检验的基本思想、方法及其简单应用和概率等知识,考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
某学校课题小组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
若单科成绩85分以上(含85分),则该科成绩为优秀.
(1)根据上表完成下面的2×2列联表(单位:人):
(2)根据题(1)中表格的数据计算,有多大的把握,认为学生的数学成绩与物理成绩之间有关系?
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率.
参考数据:
①假设有两个分类变量X和Y,它们的值域分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:
则随机变量 ,其中n=a+b+c+d为样本容量;
,其中n=a+b+c+d为样本容量;
②独立检验随机变量K2的临界值参考表:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
(1)根据上表完成下面的2×2列联表(单位:人):
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | |||
| 物理成绩不优秀 | |||
| 合计 | 20 |
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率.
参考数据:
①假设有两个分类变量X和Y,它们的值域分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:
| y1 | y2 | 合计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 合计 | a+c | b+d | a+b+c+d |
 ,其中n=a+b+c+d为样本容量;
,其中n=a+b+c+d为样本容量;②独立检验随机变量K2的临界值参考表:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某学校课题小组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
若单科成绩85分以上(含85分),则该科成绩为优秀.
(1)根据上表完成下面的2×2列联表(单位:人):
(2)根据题(1)中表格的数据计算,有多大的把握,认为学生的数学成绩与物理成绩之间有关系?
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率.
参考数据:
①假设有两个分类变量X和Y,它们的值域分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:
则随机变量 ,其中n=a+b+c+d为样本容量;
,其中n=a+b+c+d为样本容量;
②独立检验随机变量K2的临界值参考表:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
(1)根据上表完成下面的2×2列联表(单位:人):
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | |||
| 物理成绩不优秀 | |||
| 合计 | 20 |
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率.
参考数据:
①假设有两个分类变量X和Y,它们的值域分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:
| y1 | y2 | 合计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 合计 | a+c | b+d | a+b+c+d |
 ,其中n=a+b+c+d为样本容量;
,其中n=a+b+c+d为样本容量;②独立检验随机变量K2的临界值参考表:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某学校课题小组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
若单科成绩85分以上(含85分),则该科成绩为优秀.
(1)根据上表完成下面的2×2列联表(单位:人):
(2)根据题(1)中表格的数据计算,有多大的把握,认为学生的数学成绩与物理成绩之间有关系?
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率.
参考数据:
①假设有两个分类变量X和Y,它们的值域分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:
则随机变量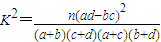 ,其中n=a+b+c+d为样本容量;
,其中n=a+b+c+d为样本容量;
②独立检验随机变量K2的临界值参考表:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
(1)根据上表完成下面的2×2列联表(单位:人):
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | |||
| 物理成绩不优秀 | |||
| 合计 | 20 |
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率.
参考数据:
①假设有两个分类变量X和Y,它们的值域分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:
| y1 | y2 | 合计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 合计 | a+c | b+d | a+b+c+d |
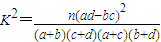 ,其中n=a+b+c+d为样本容量;
,其中n=a+b+c+d为样本容量;②独立检验随机变量K2的临界值参考表:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某学校课题小组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
若单科成绩85分以上(含85分),则该科成绩为优秀.
(1)根据上表完成下面的2×2列联表(单位:人):
(2)根据题(1)中表格的数据计算,有多大的把握,认为学生的数学成绩与物理成绩之间有关系?
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率.
参考数据:
①假设有两个分类变量X和Y,它们的值域分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:
则随机变量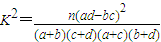 ,其中n=a+b+c+d为样本容量;
,其中n=a+b+c+d为样本容量;
②独立检验随机变量K2的临界值参考表:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
(1)根据上表完成下面的2×2列联表(单位:人):
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | |||
| 物理成绩不优秀 | |||
| 合计 | 20 |
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率.
参考数据:
①假设有两个分类变量X和Y,它们的值域分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:
| y1 | y2 | 合计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 合计 | a+c | b+d | a+b+c+d |
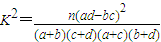 ,其中n=a+b+c+d为样本容量;
,其中n=a+b+c+d为样本容量;②独立检验随机变量K2的临界值参考表:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |