题目内容
已知抛物线C: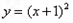 与圆
与圆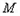 :
: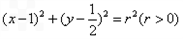 有一个公共点
有一个公共点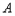 ,且在
,且在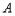 处两曲线的切线为同一直线上。
处两曲线的切线为同一直线上。
(Ⅰ)求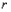 ;
;
(Ⅱ)设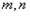 是异于
是异于 且与
且与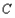 及
及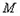 都切的两条直线,
都切的两条直线,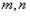 的交点为
的交点为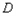 ,求
,求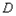 到
到 的距离。
的距离。
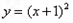 与圆
与圆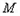 :
: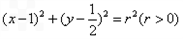 有一个公共点
有一个公共点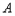 ,且在
,且在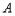 处两曲线的切线为同一直线上。
处两曲线的切线为同一直线上。(Ⅰ)求
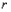 ;
;(Ⅱ)设
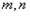 是异于
是异于 且与
且与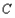 及
及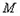 都切的两条直线,
都切的两条直线,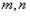 的交点为
的交点为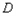 ,求
,求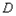 到
到 的距离。
的距离。解:(1)设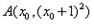 ,对
,对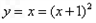 求导得
求导得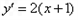 ,故直线
,故直线 的斜率
的斜率 ,
,
当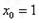 时,不合题意,
时,不合题意,
所心
圆心为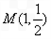 ,
,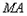 的斜率
的斜率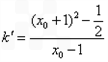
由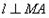 知
知 ,即
,即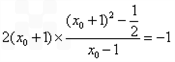 ,
,
解得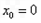 ,故
,故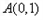
所以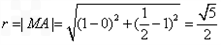 。
。
(2)设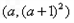 为
为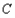 上一点,则在该点处的切线方程为
上一点,则在该点处的切线方程为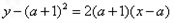
即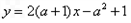 若该直线与圆
若该直线与圆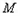 相切,则圆心
相切,则圆心 到该切线的距离为
到该切线的距离为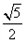 ,
,
即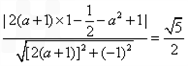 ,化简可得
,化简可得
求解可得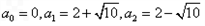
抛物线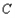 在点
在点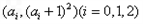 处的切线分别为
处的切线分别为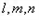 ,
,
其方程分别为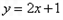 ①
①
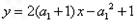 ②
②
 ③
③
②-③得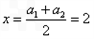 ,
,
将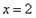 代入②得
代入②得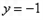 ,
,
故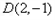 所以
所以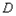 到直线
到直线 的距离为
的距离为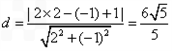 。
。
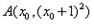 ,对
,对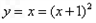 求导得
求导得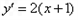 ,故直线
,故直线 的斜率
的斜率 ,
,当
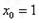 时,不合题意,
时,不合题意,所心

圆心为
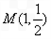 ,
,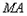 的斜率
的斜率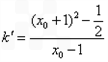
由
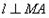 知
知 ,即
,即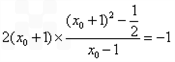 ,
,解得
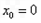 ,故
,故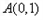
所以
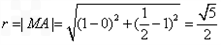 。
。(2)设
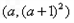 为
为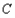 上一点,则在该点处的切线方程为
上一点,则在该点处的切线方程为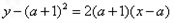
即
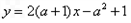 若该直线与圆
若该直线与圆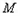 相切,则圆心
相切,则圆心 到该切线的距离为
到该切线的距离为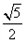 ,
,即
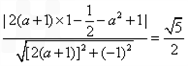 ,化简可得
,化简可得
求解可得
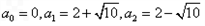
抛物线
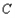 在点
在点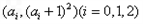 处的切线分别为
处的切线分别为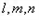 ,
,其方程分别为
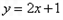 ①
① 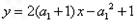 ②
②  ③
③②-③得
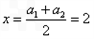 ,
,将
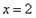 代入②得
代入②得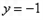 ,
,故
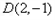 所以
所以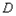 到直线
到直线 的距离为
的距离为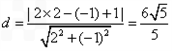 。
。
练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

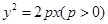 的准线与圆
的准线与圆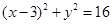 相切,则p的值为
相切,则p的值为 (B)1 (C)2 (D)4
(B)1 (C)2 (D)4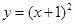 与圆
与圆 有一个公共点A,且在A处两曲线的切线与同一直线l
有一个公共点A,且在A处两曲线的切线与同一直线l