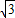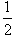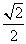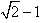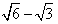题目内容
已知椭圆中心为坐标原点O,对称轴为坐标轴,左焦点F1,右顶点和上顶点分别是A,B,P为椭圆上的点,当PF1⊥x轴,且PO∥AB时,椭圆的离心率为( )
A.
| B.
| C.
| D.
|
设椭圆方程为
+
=1(a>b>0),
可得F1(-c,0),c2=a2-b2,则P(-c,b
),即P(-c,
).
∵AB∥PO,∴kAB=kOP,
即-
=-
,解得b=c.
两边平方,得b2=a2-c2=c2,解得a=
c
∴椭圆的离心率为e=
=
故选:B
| x2 |
| a2 |
| y2 |
| b2 |
可得F1(-c,0),c2=a2-b2,则P(-c,b
1-
|
| b2 |
| a |
∵AB∥PO,∴kAB=kOP,
即-
| b |
| a |
| b2 |
| ac |
两边平方,得b2=a2-c2=c2,解得a=
| 2 |
∴椭圆的离心率为e=
| c |
| a |
| ||
| 2 |
故选:B

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

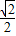
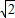 -1
-1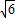 -
-