题目内容
在 中,三个内角
中,三个内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,其中
,其中 , 且
, 且
(1)求证: 是直角三角形;
是直角三角形;
(2)如图6,设圆 过
过 三点,点
三点,点 位于劣弧上,求
位于劣弧上,求 面积最大值.
面积最大值.

 中,三个内角
中,三个内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,其中
,其中 , 且
, 且
(1)求证:
 是直角三角形;
是直角三角形;(2)如图6,设圆
 过
过 三点,点
三点,点 位于劣弧上,求
位于劣弧上,求 面积最大值.
面积最大值.
(1)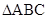 是直角三角形;(2)
是直角三角形;(2) .
.
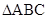 是直角三角形;(2)
是直角三角形;(2) .
.本试题主要考查相似三角形和圆的性质的综合运用,求解面积的最值和证明三角形为直角三角形

(1)证明:由正弦定理得, …………………………………2分
…………………………………2分
整理为 ,即
,即 ………………………3分
………………………3分
又因为
∴ 或
或 ,即A=B或
,即A=B或 …………6分
…………6分
∵ ∴A=B舍去,故
∴A=B舍去,故
由 可知
可知 ,∴
,∴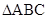 是直角三角形……………6分
是直角三角形……………6分
(2)由(1)及c=2,得a=1,b= , ……………7分
, ……………7分
设 ,则
,则 , ……………8分
, ……………8分
在 中,
中,
所以
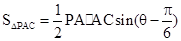 =
=
= ……………10分
……………10分
= ………………………12分
………………………12分
因为 所以
所以 ,
,
当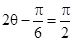 ,即
,即 时,
时, 最大值等于
最大值等于 .…………………………………14分
.…………………………………14分

(1)证明:由正弦定理得,
 …………………………………2分
…………………………………2分整理为
 ,即
,即 ………………………3分
………………………3分又因为

∴
 或
或 ,即A=B或
,即A=B或 …………6分
…………6分∵
 ∴A=B舍去,故
∴A=B舍去,故
由
 可知
可知 ,∴
,∴ 是直角三角形……………6分
是直角三角形……………6分(2)由(1)及c=2,得a=1,b=
 , ……………7分
, ……………7分设
 ,则
,则 , ……………8分
, ……………8分在
 中,
中,
所以
 =
==
 ……………10分
……………10分=
 ………………………12分
………………………12分因为
 所以
所以 ,
,当
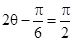 ,即
,即 时,
时, 最大值等于
最大值等于 .…………………………………14分
.…………………………………14分
练习册系列答案
相关题目
 )sin2x+
)sin2x+ sin(x+
sin(x+ )sin(x-
)sin(x- ,
, ]上的取值范围;
]上的取值范围; =2时,f(
=2时,f( ,求
,求
 的值;
的值; 求
求 的值.
的值. ,则
,则 =_________.
=_________. cos
cos -cos
-cos sin
sin 的值是
的值是  的值是 。
的值是 。 ,
, ,则函数
,则函数 的最小正周期为 .
的最小正周期为 . ,则
,则
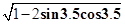 化简结果为( )
化简结果为( )