题目内容
已知函数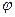 (x)=f(x)+g(x),其中f(x)是x的正比例函数,g(x)是x的反比例函数,
(x)=f(x)+g(x),其中f(x)是x的正比例函数,g(x)是x的反比例函数,
且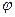 (
(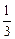 )=16,
)=16,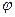 (1)=8.
(1)=8.
小题1:求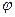 (x)的解析式,并指出定义域;
(x)的解析式,并指出定义域;
小题2:求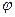 (x)的值域.
(x)的值域.
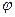 (x)=f(x)+g(x),其中f(x)是x的正比例函数,g(x)是x的反比例函数,
(x)=f(x)+g(x),其中f(x)是x的正比例函数,g(x)是x的反比例函数,且
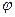 (
(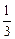 )=16,
)=16,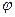 (1)=8.
(1)=8.小题1:求
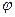 (x)的解析式,并指出定义域;
(x)的解析式,并指出定义域;小题2:求
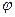 (x)的值域.
(x)的值域.小题1:设f(x)=ax,g(x)=
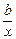 ,a、b为比例常数,则
,a、b为比例常数,则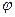 (x)=f(x)+g(x)=ax+
(x)=f(x)+g(x)=ax+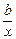
由
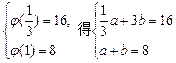 ,解得
,解得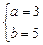
∴
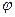 (x)=3x+
(x)=3x+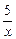 ,其定义域为(-∞,0)∪(0,+∞)
,其定义域为(-∞,0)∪(0,+∞)小题2:由y =3x+
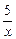 ,得3x2-yx+5=0(x≠0)
,得3x2-yx+5=0(x≠0)∵x∈R且x≠0,∴Δ=y2-60≥0,∴y≥2
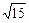 或y≤-2
或y≤-2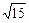
∴
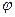 (x) 的值域为(-∞,-2
(x) 的值域为(-∞,-2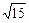
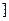 ∪[2
∪[2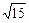 ,+∞
,+∞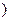
同答案

练习册系列答案
相关题目
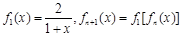 ,且
,且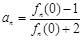 ,则
,则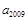 等于( )
等于( )
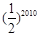
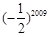
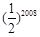
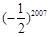
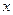
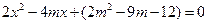

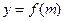
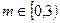
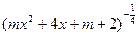 +(x2-mx+1)的定义域为全体实数,则m的取值范围是( )
+(x2-mx+1)的定义域为全体实数,则m的取值范围是( )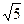 -1,2)
-1,2)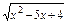 ;
;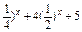 .
. 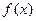 是定义在
是定义在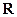 内、以
内、以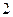 为周期的函数,当
为周期的函数,当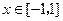 时,
时,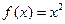 .
.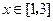 时,
时,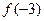 ,
,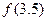 的值.
的值.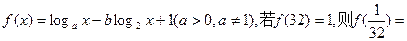 ( )
( )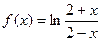 ,则函数
,则函数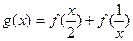 的定义域是
的定义域是 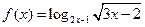 的定义域.
的定义域.