题目内容
13．计算：C${\;}_{n+1}^{3}$×C${\;}_{n}^{2-n}$．分析 根据组合数的意义，先求出n的值，再计算C${\;}_{n+1}^{3}$×C${\;}_{n}^{2-n}$．
解答 解：根据题意，得；
$\left\{\begin{array}{l}{n+1≥3}\\{2-n≥0}\\{n≥2-n}\\{n{∈N}^{*}}\end{array}\right.$，
解得n=2；
∴C${\;}_{n+1}^{3}$×C${\;}_{n}^{2-n}$=${C}_{3}^{3}$×${C}_{2}^{0}$
=1×1
=1．
点评 本题考查了组合数公式的应用问题，也考查了组合数的概念的应用问题，是基础题目．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5．
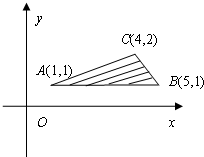在如图所示的坐标平面的可行域内（阴影部分且包括边界），若目标函数z=x+ay取得最小值的最优解有无数个，则$\frac{y}{x-a}$的最大值是（ ）
在如图所示的坐标平面的可行域内（阴影部分且包括边界），若目标函数z=x+ay取得最小值的最优解有无数个，则$\frac{y}{x-a}$的最大值是（ ）| A． | $\frac{2}{7}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{4}$ |