题目内容
函数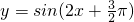 的图象
的图象
- A.关于直线
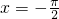 对称
对称 - B.关于直线
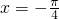 对称
对称 - C.关于直线
 对称
对称 - D.关于直线
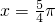 对称
对称
A
分析:利用诱导公式可将函数化为余弦型函数,进而根据余弦函数的对称性,求出函数图象对称轴方程,即可得到答案.
解答:∵函数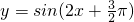 =-cos2x
=-cos2x
由余弦函数性质可得
当2x=kπ,k∈Z时函数取最值,此时x= ,k∈Z
,k∈Z
故函数的对称轴为x= ,k∈Z
,k∈Z
当k=-1时,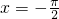
故选A
点评:本题考查的知识点是正弦函数的对称性,正弦函数的图象,其中根据弦函数取最值时,X的取值即为对称轴方程,是解答本题的关键.
分析:利用诱导公式可将函数化为余弦型函数,进而根据余弦函数的对称性,求出函数图象对称轴方程,即可得到答案.
解答:∵函数
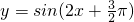 =-cos2x
=-cos2x由余弦函数性质可得
当2x=kπ,k∈Z时函数取最值,此时x=
 ,k∈Z
,k∈Z故函数的对称轴为x=
 ,k∈Z
,k∈Z当k=-1时,
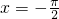
故选A
点评:本题考查的知识点是正弦函数的对称性,正弦函数的图象,其中根据弦函数取最值时,X的取值即为对称轴方程,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目