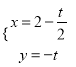题目内容
【题目】设函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() ,
, ![]() .
.
(1)若![]() 是
是![]() 的极值点,且直线
的极值点,且直线![]() 分别与函数
分别与函数![]() 和
和![]() 的图象交于
的图象交于![]() ,求
,求![]() 两点间的最短距离;
两点间的最短距离;
(2)若![]() 时,函数
时,函数![]() 的图象恒在
的图象恒在![]() 的图象上方,求实数
的图象上方,求实数![]() 的取值范围.
的取值范围.
【答案】(1)1(2)![]()
【解析】试题分析:
(1)结合题意可得|PQ|=et+sint2t.令h(x)=ex+sinx2x,结合函数的性质可得![]() 两点间的最短距离是1;
两点间的最短距离是1;
(2)构造函数![]() ,结合题意可得实数
,结合题意可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)因为F(x)=ex+sinxax,所以F′(x)=ex+cosxa,
因为x=0是F(x)的极值点,所以F′(0)=1+1a=0,a=2.
又当a=2时,若x<0,F′(x)=ex+cosxa<1+12=0,
所以F′(x)在(0,+∞)上为增函数,所以F′(x)>F′(0)=1+12=0,所以x=0是F(x)的极小值点,
所以a=2符合题意,所以|PQ|=et+sint2t.令h(x)=ex+sinx2x,即h′(x)=ex+cosx2,
因为h′′(x)=exsinx,当x>0时,ex>1,1sinx1,
所以h′′(x)=exsinx>0,所以h′(x)=ex+cosx2在(0,+∞)上递增,
所以h′(x)=ex+cosx2>h′(0)=0,∴x∈[0,+∞)时,h(x)的最小值为h(0)=1,所以|PQ|min=1.
(2)令![]() ,
,
则![]() ,
,
![]() ,
,
因为![]() 当
当![]() 时恒成立,
时恒成立,
所以函数![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() 当
当![]() 时恒成立;
时恒成立;
故函数![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 在
在![]() 时恒成立.
时恒成立.
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 单调递增,即
单调递增,即![]() .
.
故![]() 时
时![]() 恒成立.
恒成立.
当![]() 时,因为
时,因为![]() 在
在![]() 单调递增,所以总存在
单调递增,所以总存在![]() ,使
,使![]() 在区间
在区间![]() 上
上![]() ,导致
,导致![]() 在区间
在区间![]() 上单调递减,而
上单调递减,而![]() ,所以当
,所以当![]() 时,
时, ![]() ,这与
,这与![]() 对
对![]() 恒成立矛盾,所以
恒成立矛盾,所以![]() 不符合题意,故符合条件的
不符合题意,故符合条件的![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目