题目内容
(1)若抛物线的焦点是椭圆| x2 |
| 64 |
| y2 |
| 16 |
(2)若双曲线与椭圆
| x2 |
| 64 |
| y2 |
| 16 |
| y2 |
| 2 |
| x2 |
| 6 |
分析:(1)先根据椭圆中的a的值求得c值,从而出左顶点的坐标,再根据抛物线的顶点在坐标原点,焦点是 (-8,0)的位置,求得抛物线方程中的p,抛物线方程可得.
(2)由题意得,c=4
,
=
,48=a2+b2,解出a和b的值,即得所求的双曲线的标准方程.
(2)由题意得,c=4
| 3 |
| b |
| a |
| 4 |
| 3 |
解答:解:(I)椭圆
+
=1的左顶点为(-8,0),
∴抛物线的焦点为(-8,0),(2分)
设抛物线方程为y2=-2px(p>0),
则-
=-8,p=16,(4分)
∴所求抛物线的标准方程为y2=-32x.(6分)
(II)椭圆
+
=1的焦点为F1(-4
,0),F2(4
,0),(8分)
双曲线
-
=1的渐近线方程为y=±
x,(10分)
设所求双曲线方程为
-
=1(a>0,b>0),
由题意知:
(12分)
∴
∴所求双曲线方程为
-
=1.(14分)
| x2 |
| 64 |
| y2 |
| 16 |
∴抛物线的焦点为(-8,0),(2分)
设抛物线方程为y2=-2px(p>0),
则-
| p |
| 2 |
∴所求抛物线的标准方程为y2=-32x.(6分)
(II)椭圆
| x2 |
| 64 |
| y2 |
| 16 |
| 3 |
| 3 |
双曲线
| y2 |
| 2 |
| x2 |
| 6 |
| ||
| 3 |
设所求双曲线方程为
| x2 |
| a2 |
| y2 |
| b2 |
由题意知:
|
∴
|
∴所求双曲线方程为
| x2 |
| 36 |
| y2 |
| 12 |
点评:本题主要考查了椭圆的简单性质和抛物线的标准方程.解答的关键在于考生对圆锥曲线的基础知识的把握.

练习册系列答案
相关题目

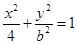 (0<b<2)的离心率等于
(0<b<2)的离心率等于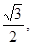 抛物线
抛物线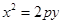 (p>0).
(p>0).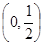 ,在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足
,在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足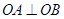 ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.