题目内容
已知一个 数列的各项是1或2,首项为1,且在第k个1和第k+1个1之间有2k-1个2,如:1,2,1,2,2,1,2,2,2,2,1,2,2,2,2,2,2,2,2,1,…则该数列前2009项的和S2009=
4007
4007
.分析:先将数列分组,便于发现规律,如分为(1,2),(1,2,2),(1,2,2,2,2)…,每组的项数构成数列2,3,5,9…,2n-1+1,再计算第2009项处于第几组的第几个数,最后数列分组求和即可
解答:解:此数列可分若干组(1,2),(1,2,2),(1,2,2,2,2)…,每组的项数构成数列2,3,5,9…,2n-1+1
由2+3+5+9+…+2n-1+1=1+1+2+1+4+1+…+2n-1+1=n+
=n+2n-1≤2009,得n≤10,
故第10组的最后一个2是第1033项,1034项为1,后边有210项2,第975个2是数列的第2009项
故S2009=11+2(1+2+22+…+29+975)=4007
故答案为4007
由2+3+5+9+…+2n-1+1=1+1+2+1+4+1+…+2n-1+1=n+
| 1×(2n-1) |
| 2-1 |
故第10组的最后一个2是第1033项,1034项为1,后边有210项2,第975个2是数列的第2009项
故S2009=11+2(1+2+22+…+29+975)=4007
故答案为4007
点评:本题考察了观察法求数列的通项公式,数列求和方法等知识,解题时要善于发现规律,层层深入的解决问题,要有较强的运算能力

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
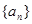 的各项都是1或2.首项为1,且在第
的各项都是1或2.首项为1,且在第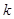 个1和第
个1和第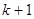 个1之间有
个1之间有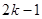 个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前
个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前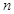 项的和为
项的和为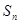 .参考:31×32=992,32×33=1056,44×45=1980,45×46=2070
.参考:31×32=992,32×33=1056,44×45=1980,45×46=2070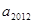 和
和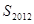 ;
;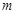 ,使得
,使得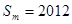 ?如果存在,求出
?如果存在,求出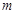 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由. 的各项都是1或2.首项为1,且在第
的各项都是1或2.首项为1,且在第 个1和第
个1和第 个1之间有
个1之间有 个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前
个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前 项的和为
项的和为 .
. 和
和 ;
; ,使得
,使得 ?如果存在,求出
?如果存在,求出