题目内容
如图,在三棱柱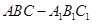 中,
中,  ,
, ,
,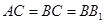 ,点
,点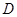 是
是 的中点,
的中点,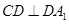 .
.

(Ⅰ)求证: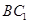 ∥平面
∥平面 ;
;
(Ⅱ)设点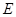 在线段
在线段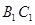 上,
上,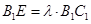 ,且使直线
,且使直线 和平面
和平面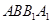 所成的角的正弦值为
所成的角的正弦值为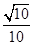 ,求
,求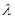 的值.
的值.
【答案】
(Ⅰ)连接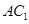 交
交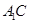 于点
于点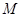 ,连接
,连接 ,得到
,得到 ∥
∥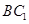 ,进一步可得
,进一步可得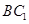 ∥平面
∥平面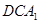 .
.
(Ⅱ) 。
。
【解析】
试题分析:(Ⅰ)证明:在三棱柱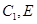 中,
中,
连接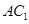 交
交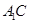 于点
于点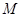 ,连接
,连接 ,则
,则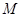 是
是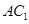 的中点
的中点
在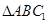 中,点
中,点 是
是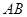 的中点,
的中点,
所以 ∥
∥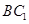 ,
,
又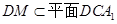 ,
,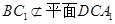 ,
,
所以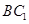 ∥平面
∥平面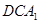 . (5分)
. (5分)
(Ⅱ)在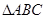 中,
中, ,
,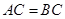 ,点
,点 是
是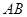 的中点
的中点
所以 ,又
,又 ,
,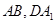 是平面
是平面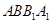 内的相交直线,
内的相交直线,
所以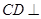 平面
平面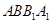 ,可知
,可知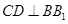 . (7分)
. (7分)
又 ,
, 是平面
是平面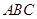 内的相交直线,交点是D,
内的相交直线,交点是D,
知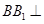 平面
平面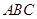 .
. 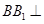 平面
平面
在三棱柱 中,
中,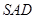 为线段
为线段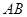 上的点,
上的点,
过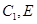 分别作
分别作 于点
于点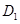 ,
,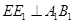 于点
于点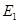 ,连接
,连接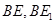
由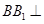 平面
平面 ,
, ,得
,得
又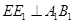 ,
,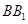 、
、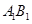 是平面
是平面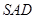 内的相交直线
内的相交直线
所以 平面
平面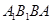 ,
,
 是
是 在平面
在平面 内的射影,
内的射影,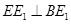
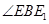 是直线
是直线 和平面
和平面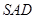 所成的角. (12分)
所成的角. (12分)
设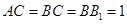 ,由
,由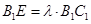 得
得
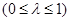 ,
,
可得 ,
,
所以在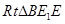 中,
中,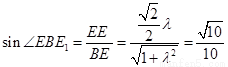 , 解得
, 解得 (14分)
(14分)
考点:三棱柱的几何特征,平行关系,垂直关系,角的计算。
点评:中档题,立体几何问题中,平行关系、垂直关系,角、距离、面积、体积等的计算,是常见题型,基本思路是将空间问题转化成为平面问题,利用平面几何知识加以解决。要注意遵循“一作,二证,三计算”。利用“向量法”,通过建立空间直角坐标系,往往能简化解题过程。

练习册系列答案
相关题目
 如图,在三棱柱中,已知AB⊥侧面BB1C1C,
如图,在三棱柱中,已知AB⊥侧面BB1C1C,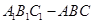 中,
中,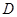 ,
,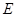 ,
,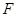 分别为
分别为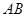 ,
, ,
,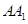 的中点,设三棱锥
的中点,设三棱锥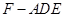 体积为
体积为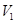 ,三棱柱
,三棱柱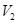 ,则
,则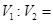

 中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则
中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则 与平面
与平面 所成的角是
所成的角是
 B.
B. C.
C.  D.
D.
 中,
中, 侧面
侧面 ,且
,且 与底面成
与底面成 角,
角, ,则该棱柱体积的 最小值为
.
,则该棱柱体积的 最小值为
. 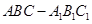 中,
中,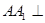 面
面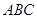 ,
,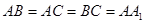 ,
,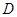 ,
,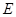 分别为
分别为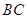 ,
,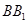 的中点.
的中点.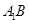 ∥平面
∥平面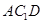 ; (2)求证:
; (2)求证: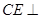 平面
平面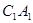 与平面
与平面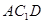 所成的角的正弦值.
所成的角的正弦值.