题目内容
6.小军旅行箱的密码是一个六位数,由于他忘记了密码的末位数字,则小军能一次打开该旅行箱的概率是( )| A. | $\frac{1}{10}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{5}$ |
分析 小军密码的末位数有0,1,2,3,4,5,6,7,8,9,共10种可能,由此能求出小军能一次打开该旅行箱的概率.
解答 解:∵小军旅行箱的密码是一个六位数,由于他忘记了密码的末位数字,
∴小军密码的末位数有0,1,2,3,4,5,6,7,8,9,共10种可能,
∴小军能一次打开该旅行箱的概率p=$\frac{1}{10}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
17.在复平面内,复数z和$\frac{1+i}{1-2i}$所表示的点关于虚轴对称,则z=( )
| A. | -$\frac{1}{5}$+$\frac{3}{5}$i | B. | $\frac{1}{5}$+$\frac{3}{5}$i | C. | $\frac{1}{5}$-$\frac{3}{5}$i | D. | -$\frac{1}{5}$-$\frac{3}{5}$i |
14.设${a_n}={n^2}-2kn+6$(n∈N*,k∈R)
(1)证明:k≤1是{an}为递增数列的充分不必要条件;
(2)若$?n∈{N^*},\frac{a_n}{n}≥1$,求k的取值范围.
(1)证明:k≤1是{an}为递增数列的充分不必要条件;
(2)若$?n∈{N^*},\frac{a_n}{n}≥1$,求k的取值范围.
1.在△ABC中,如果(b+c+a)(b+c-a)=bc,那么A等于( )
| A. | 30° | B. | 120° | C. | 60° | D. | 150° |
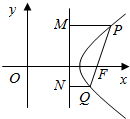 如图,点F是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,过点F的直线的斜率为3,与双曲线交于P,Q两点,分别过P、Q向右准线作垂线,垂足分别为M,N,且$\overrightarrow{PM}$=3$\overrightarrow{QN}$,求双曲线的离心率的大小.
如图,点F是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,过点F的直线的斜率为3,与双曲线交于P,Q两点,分别过P、Q向右准线作垂线,垂足分别为M,N,且$\overrightarrow{PM}$=3$\overrightarrow{QN}$,求双曲线的离心率的大小.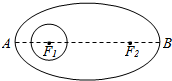 1998年12月19日,太原卫星发射中心为摩托罗拉公司(美国)发射了“铱星”系统通信卫星,卫星运行的轨道是椭圆,F1、F2是其焦点,地球中心为焦点F1,设地球半径为m,已知椭圆轨道的近地点A(离地面最近的点)距地面$\frac{m}{3}$,远地点B(离地面最远的点)距地面3m,并且F1、A、B在同一直线上,求卫星运行的轨道方程.
1998年12月19日,太原卫星发射中心为摩托罗拉公司(美国)发射了“铱星”系统通信卫星,卫星运行的轨道是椭圆,F1、F2是其焦点,地球中心为焦点F1,设地球半径为m,已知椭圆轨道的近地点A(离地面最近的点)距地面$\frac{m}{3}$,远地点B(离地面最远的点)距地面3m,并且F1、A、B在同一直线上,求卫星运行的轨道方程.