题目内容
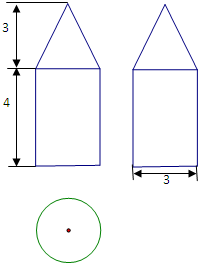 如图是一个几何体的三视图,根据图中数据,可得该几何体的体积是
如图是一个几何体的三视图,根据图中数据,可得该几何体的体积是分析:易得此几何体为一个圆柱和圆锥的组合题,根据图中数据我们易得到圆柱与圆锥的底面直径和高,根据圆锥体积=
×底面积×高,圆柱体积=底面积×高,把相关数值代入即可求解.
| 1 |
| 3 |
解答:解:由主视图和左视图为等腰三角形+一个矩形,可得此几何体为锥体+柱体,
由俯视图为圆可得此几何体为圆锥+圆柱,
∵主视图三角形高为3,矩形高为4
∴圆锥的高为 3,圆柱的高为4,
又∵侧视图的底边长为3,
∴圆柱与圆锥的底面直径为3,
∴底面面积为:
π
∴组合体的体积=
×
π×3+
π×4=
π
故答案:
π
由俯视图为圆可得此几何体为圆锥+圆柱,
∵主视图三角形高为3,矩形高为4
∴圆锥的高为 3,圆柱的高为4,
又∵侧视图的底边长为3,
∴圆柱与圆锥的底面直径为3,
∴底面面积为:
| 9 |
| 4 |
∴组合体的体积=
| 1 |
| 3 |
| 9 |
| 4 |
| 9 |
| 4 |
| 45 |
| 4 |
故答案:
| 45 |
| 4 |
点评:本题考查的知识点是由三视图求体积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目

 (2012•马鞍山二模)如图是一个几何体的三视,则它的表面为( )
(2012•马鞍山二模)如图是一个几何体的三视,则它的表面为( )
 π
π π
π
 A.
A.


