题目内容
若AB=2,AC=| 2 |
分析:设BC=x,根据面积公式用x和sinB表示出三角形的面积,再根据余弦定理用x表示出sinB,代入三角形的面积表达式,进而得到关于x的三角形面积表达式,再根据三角形的两边之和大于第三边列出关于x的不等式,求出不等式的解集得到x的范围,根据x的范围求出被开方数中完全平方式为0时的x的值,把求出x的值代入即可得到三角形面积的最大值.
解答:解:设BC=x,则AC=
x,
根据面积公式得S△ABC=
AB•BCsinB=
×2x×
,
又根据余弦定理得cosB=
=
=
,
代入上式得:
S△ABC=x
=
,
由三角形三边关系有:
,
解得:2
-2<x<2
+2.
所以当x=2
时,x2-12=0,此时S△ABC取得最大值
=
=2
.
故答案为:2
| 2 |
根据面积公式得S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1-cos2B |
又根据余弦定理得cosB=
| AB2+BC2-AC2 |
| 2AB•BC |
4+x2-(
| ||
| 4x |
| 4-x2 |
| 4x |
代入上式得:
S△ABC=x
1-(
|
|
由三角形三边关系有:
|
解得:2
| 2 |
| 2 |
所以当x=2
| 3 |
|
| 8 |
| 2 |
故答案为:2
| 2 |
点评:本题主要考查了余弦定理和面积公式在解三角形中的应用,当涉及最值问题时,可考虑用函数的单调性和定义域等问题,本题的思路为:利用三角形的任两边之和大于第三边列出不等式,求出x的范围,进而根据x的范围求出完全平方式的最小值即为三角形面积的最大值.

练习册系列答案
相关题目
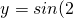 图象向右平移
图象向右平移 个单位,得到函数y=sin2x的图象;
个单位,得到函数y=sin2x的图象;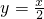 的图象有三个公共点.
的图象有三个公共点.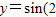 图象向右平移
图象向右平移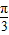 个单位,得到函数y=sin2x的图象;
个单位,得到函数y=sin2x的图象;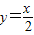 的图象有三个公共点.
的图象有三个公共点.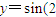 图象向右平移
图象向右平移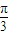 个单位,得到函数y=sin2x的图象;
个单位,得到函数y=sin2x的图象;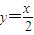 的图象有三个公共点.
的图象有三个公共点.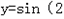 图象向右平移
图象向右平移 个单位,得到函数y=sin2x的图象;
个单位,得到函数y=sin2x的图象;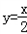 的图象有三个公共点.
的图象有三个公共点.