题目内容
若函数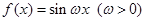
在区间
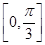上单调递增，在区间
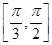上单调递减，则
＝ ▲
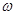【答案】
【解析】略
练习册系列答案
相关题目
的单调区间；
，在（1，2）上为单调递已知函数
，（
），
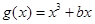
（1）若曲线
与曲线
在它们的交点（1，c）处具有公共切线，求a,b的值
（2）当
时，若函数
的单调区间，并求其在区间（-∞，-1）上的最大值。
【解析】（1）
，
∵曲线与曲线在它们的交点（1，c）处具有公共切线
∴
，
∴
（2）令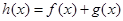
，当
时，
令
，得
时，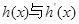
的情况如下：
|
x |
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
|
|
|
所以函数
的单调递增区间为
，
，单调递减区间为
当
，即
时，函数在区间
上单调递增，在区间上的最大值为
，
当
且
，即
时，函数在区间内单调递增，在区间
上单调递减，在区间上的最大值为
当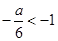
，即a>6时，函数在区间内单调递赠，在区间内单调递减，在区间
上单调递增。又因为
所以在区间上的最大值为。
(ω>0)在区间
上单调递 增，在区间
上单调递减，则
( )
B．
C． 2 D．3