题目内容
设 是右焦点为F的椭圆
是右焦点为F的椭圆 上三个不同的点,则“|AF|,|BF|,|CF|成等差数列”是“x1+x2=8”的( )
上三个不同的点,则“|AF|,|BF|,|CF|成等差数列”是“x1+x2=8”的( )A.充要条件
B.必要不充分条件
C.充分不必要条件
D.既非充分也非必要
【答案】分析:先根据椭圆方程求得右准线方程,进而分别求得A、B、C到右准线的距离进而根据椭圆的第二定义用e和点到准线的距离表示出|AF|,|BF|,|CF|,进而可知丨AF丨,丨BF丨,丨CF丨成等差数列等价于2ed2=ed1+ed3,2d2=d1+d3,即:x1+x2=8推断出结论.
解答:解:右准线为:x= =
=
设A、B、C到右准线的距离为d1、d2、d3
d1= -x1,d2=
-x1,d2= ,d3=
,d3= -x2
-x2
由椭圆的第二定义(点到定点的距离等于到定直线距离的e倍,定点为焦点,定直线为准线)
丨AF丨=ed1、丨BF丨=ed2、丨CF丨=ed3
丨AF丨,丨BF丨,丨CF丨成等差数列等价于2ed2=ed1+ed3,2d2=d1+d3,即:x1+x2=8
∴“丨AF丨,丨BF丨,丨CF丨成等差数列”是“X1+X2=8的充要条件.
点评:这道题目综合考查了解析几何中椭圆的性质(人教版选修2-1第三章)与简易逻辑中的命题的基本关系(人教版选修2-1第一章),可以认为这是一道以简易逻辑为背景的解析几何题目.
解答:解:右准线为:x=
 =
=
设A、B、C到右准线的距离为d1、d2、d3
d1=
 -x1,d2=
-x1,d2= ,d3=
,d3= -x2
-x2由椭圆的第二定义(点到定点的距离等于到定直线距离的e倍,定点为焦点,定直线为准线)
丨AF丨=ed1、丨BF丨=ed2、丨CF丨=ed3
丨AF丨,丨BF丨,丨CF丨成等差数列等价于2ed2=ed1+ed3,2d2=d1+d3,即:x1+x2=8
∴“丨AF丨,丨BF丨,丨CF丨成等差数列”是“X1+X2=8的充要条件.
点评:这道题目综合考查了解析几何中椭圆的性质(人教版选修2-1第三章)与简易逻辑中的命题的基本关系(人教版选修2-1第一章),可以认为这是一道以简易逻辑为背景的解析几何题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
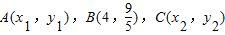 是右焦点为F的椭圆
是右焦点为F的椭圆 上三个不同的点,则“|AF|,|BF|,|CF|成等差数列”是“x1+x2=8”的( )
上三个不同的点,则“|AF|,|BF|,|CF|成等差数列”是“x1+x2=8”的( ) 是右焦点为F的椭圆
是右焦点为F的椭圆 上三个不同的点,则“|AF|,|BF|,|CF|成等差数列”是“x1+x2=8”的( )
上三个不同的点,则“|AF|,|BF|,|CF|成等差数列”是“x1+x2=8”的( ) 是右焦点为F的椭圆
是右焦点为F的椭圆 上三个不同的点,则“|AF|,|BF|,|CF|成等差数列”是“x1+x2=8”的( )
上三个不同的点,则“|AF|,|BF|,|CF|成等差数列”是“x1+x2=8”的( ) 是右焦点为F的椭圆
是右焦点为F的椭圆 上三个不同的点,则“|AF|,|BF|,|CF|成等差数列”是“x1+x2=8”的( )
上三个不同的点,则“|AF|,|BF|,|CF|成等差数列”是“x1+x2=8”的( )