题目内容
(10分)
已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ<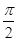 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为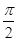 ,且图象上一个最低点为
,且图象上一个最低点为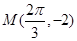
(1)求A,ω,φ的值.(2)写出函数f(x)图象的对称中心及单调递增区间.
(3)当x∈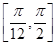 时,求f(x)的值域.
时,求f(x)的值域.
【答案】
(1)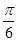 ;(2)(
;(2)(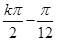 ,0),
,0),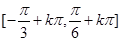 ,
, 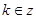 (3)([-1,2])
(3)([-1,2])
【解析】(1)根据与x轴的相邻两个交点之间的距离可得半个周期的长度,进而求出周期,确定出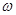 值.再根据最低点,确定A,及
值.再根据最低点,确定A,及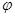 的值.
的值.
(2)在(1)的基础上,可利用基本的正弦函数y=sinx的中心坐标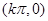 ,
,
单调增区间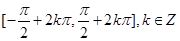 来求此函数的对称中心及单调增区间.
来求此函数的对称中心及单调增区间.
(3)根据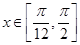 ,求出
,求出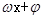 的取值范围,进而可求出f(x)的值域.
的取值范围,进而可求出f(x)的值域. 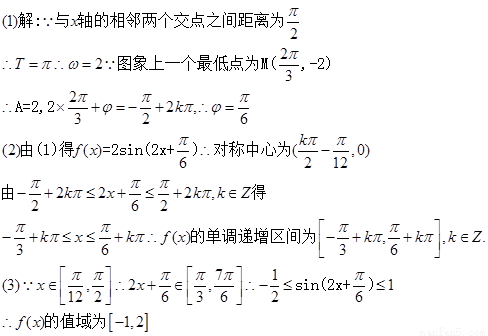

练习册系列答案
相关题目
 )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有