题目内容
已知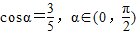 .
.(Ⅰ)求
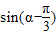 的值
的值(Ⅱ)把
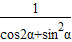 用tanα表示出来,并求其值.
用tanα表示出来,并求其值.
【答案】分析:(Ⅰ)利用同角三角函数的基本关系式,求出sinα,利用两角和的正弦函数求出所求表达式的值.
(Ⅱ)求出tanα的值,利用同角三角函数的基本关系式,表示分子,然后化为tanα的形式,求解即可.
解答:解:(Ⅰ)已知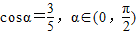 .
.
所以sinα= ,
,
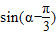 =sinαcos
=sinαcos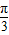 -cosαsin
-cosαsin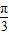 =
=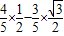 =
=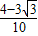 .
.
(Ⅱ)因为sinα= ,
,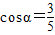 ,tanα=
,tanα= ,
,
所以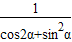 =
= =tan2α+1,
=tan2α+1,
其值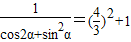 =
=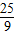 .
.
点评:本题考查同角三角函数的基本关系式,二倍角的余弦函数,两角和与差的三角函数的应用,考查计算能力.
(Ⅱ)求出tanα的值,利用同角三角函数的基本关系式,表示分子,然后化为tanα的形式,求解即可.
解答:解:(Ⅰ)已知
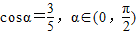 .
.所以sinα=
 ,
,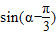 =sinαcos
=sinαcos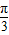 -cosαsin
-cosαsin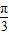 =
=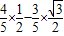 =
=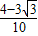 .
.(Ⅱ)因为sinα=
 ,
,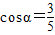 ,tanα=
,tanα= ,
,所以
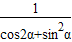 =
= =tan2α+1,
=tan2α+1,其值
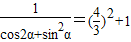 =
=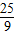 .
.点评:本题考查同角三角函数的基本关系式,二倍角的余弦函数,两角和与差的三角函数的应用,考查计算能力.

练习册系列答案
相关题目
 ,集合
,集合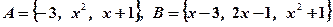
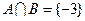 ,求
,求 的值和集合
的值和集合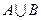 .
.
 的值;
的值; 对称,且t∈(0,π),求t的值.
对称,且t∈(0,π),求t的值.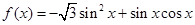
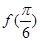 的值;
的值; 的最小正周期及最大值.
的最小正周期及最大值.