题目内容
设M={x| },N={x|x2+(a﹣8)x﹣8a≤0},命题p:x∈M,命题q:x∈N.
},N={x|x2+(a﹣8)x﹣8a≤0},命题p:x∈M,命题q:x∈N.
(1)当a=﹣6时,试判断命题p是命题q的什么条件;
(2)求a的取值范围,使命题p是命题q的一个必要但不充分条件.
 },N={x|x2+(a﹣8)x﹣8a≤0},命题p:x∈M,命题q:x∈N.
},N={x|x2+(a﹣8)x﹣8a≤0},命题p:x∈M,命题q:x∈N.(1)当a=﹣6时,试判断命题p是命题q的什么条件;
(2)求a的取值范围,使命题p是命题q的一个必要但不充分条件.
解:(1)M={x| }={x|x<﹣3或x>5},
}={x|x<﹣3或x>5},
当a=﹣6时,N={x|x2+(a﹣8)x﹣8a≤0}={x|x2﹣14x+48≤0}={x|6≤x≤8},
∵命题p:x∈M,命题q:x∈N,
∴q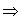 p,p推不出q,
p,p推不出q,
∴命题p是命题q的必要不充分条件.
(2)∵M={x|x<﹣3或x>5},N={x|(x﹣8)(x+a)≤0},
命题p是命题q的必要不充分条件,
∴﹣a>8,即a<﹣8时,N={x|8<x<﹣a},成立;
﹣a=8,即a=﹣8时,N={8},成立;
﹣a<8,即a>﹣8时,N={﹣a<x<8},﹣a>5,
∴a<﹣5,
综上所述,a的取值范围是{a|a<﹣5}.
 }={x|x<﹣3或x>5},
}={x|x<﹣3或x>5},当a=﹣6时,N={x|x2+(a﹣8)x﹣8a≤0}={x|x2﹣14x+48≤0}={x|6≤x≤8},
∵命题p:x∈M,命题q:x∈N,
∴q
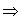 p,p推不出q,
p,p推不出q,∴命题p是命题q的必要不充分条件.
(2)∵M={x|x<﹣3或x>5},N={x|(x﹣8)(x+a)≤0},
命题p是命题q的必要不充分条件,
∴﹣a>8,即a<﹣8时,N={x|8<x<﹣a},成立;
﹣a=8,即a=﹣8时,N={8},成立;
﹣a<8,即a>﹣8时,N={﹣a<x<8},﹣a>5,
∴a<﹣5,
综上所述,a的取值范围是{a|a<﹣5}.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
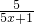 ≥1},N={x|x2-x<0},则
≥1},N={x|x2-x<0},则