题目内容
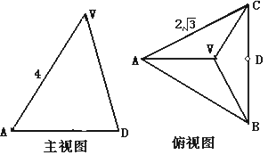
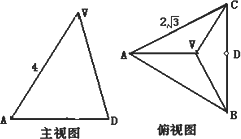
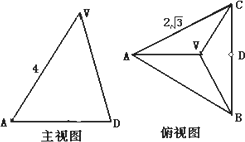
正三棱锥V-ABC的底面边长为a,侧棱与底面所成的角等于θ,过底面一边作此棱锥的截面,当截面与底面所成二面角为何值时,截面面积最小?并求出最小值.
答案:
解析:
解析:
|
如图,∵截面△PBC中,BC=a为定值,而S=
∴若使S最小,只需PD最小即可. ∵VA、BC为异面直线 ∴当PD为VA、BC的公垂线时,PD的距离即为最短. ∴当PD⊥BC,PD⊥VA时,PD最短. 在Rt△PDA中,∵∠ADP= ∵S△PBC= |

练习册系列答案
相关题目
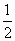 BC·PO
BC·PO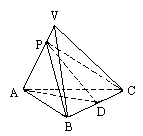
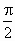 -θ ∴PD=AD·sinθ=
-θ ∴PD=AD·sinθ= asinθ
asinθ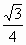 a2sinθ
a2sinθ