题目内容
已知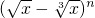
的二项展开式中所有奇数项的系数之和为512，
（1）求展开式的所有有理项（指数为整数）．
（2）求（1-x）3+（1-x）4+∧+（1-x）n展开式中x2项的系数．
解：（1）Cn0+Cn2+…=2n-1=512=29
∴n-1=9，n=10
=
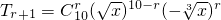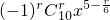（r=0，1，，10）
∵5-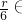
Z，∴r=0，6
有理项为T1=C100x5，T7=C106x4=210x4
（2）∵Cnr+Cnr-1=Cn+1r，
∴x2项的系数为C32+C42+…+C102=（C43-C33）+…+（C113-C103）
=C113-C33=164
分析：（1）根据二项展开式中所有奇数项的系数之和为512，写出所有系数的和的表示形式，得到n=10，写出通项式，使得通项式中x的指数等于整数，求出所有的项．
（2）根据二项式系数的性质，变形整理把一项移项，写出展开式中x2项的系数，把系数写成两项的差，依次相加得到结果．
点评：本题考查二项式定理，解题的关键是对于二项式性质的变形应用，然后依次合并同类项，得到最简结果．
∴n-1=9，n=10
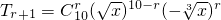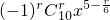=（r=0，1，，10）∵5-
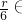Z，∴r=0，6有理项为T1=C100x5，T7=C106x4=210x4
（2）∵Cnr+Cnr-1=Cn+1r，
∴x2项的系数为C32+C42+…+C102=（C43-C33）+…+（C113-C103）
=C113-C33=164
分析：（1）根据二项展开式中所有奇数项的系数之和为512，写出所有系数的和的表示形式，得到n=10，写出通项式，使得通项式中x的指数等于整数，求出所有的项．
（2）根据二项式系数的性质，变形整理把一项移项，写出展开式中x2项的系数，把系数写成两项的差，依次相加得到结果．
点评：本题考查二项式定理，解题的关键是对于二项式性质的变形应用，然后依次合并同类项，得到最简结果．
练习册系列答案
名师点拨卷系列答案
相关题目
）（1+
）…（1+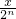
）的展开式中，x的系数为an，x2的系数为bn，其中 n∈N*．
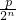（1+
）（1+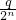
） 对n∈N*，n≥2恒成立？证明你的结论．
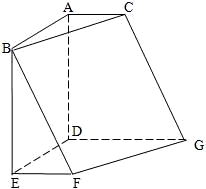如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，AB⊥AC，ED⊥DG，EF∥DG．且AB=AD=DE=DG=2，AC=EF=1．