题目内容
给定两个命题，P：关于x的方程x2-4x+a=0有实数根；Q：方程
+
=1表示焦点在x轴上的椭圆；如果P∨Q为真命题，P∧Q为假命题，求实数a的取值范围．
| x2 |
| 4-a |
| y2 |
| a-2 |
分析：先求出命题p为真，令判别式大于等于0求出a的范围，求出命题Q为真a的范围，将P∨Q为真命题，P∧Q为假命题，转化为PQ一真一假，求出a的范围．
解答：解：若命题p为真，则16-4a≥0解得a≤4（2分）
若命题Q为真，则有4-a＞a-2＞0解得2＜a＜3（2分）
由于P∨Q为真命题，P∧Q为假命题，故PQ一真一假，（2分）
故a≤2或3≤a≤4（4分）
若命题Q为真，则有4-a＞a-2＞0解得2＜a＜3（2分）
由于P∨Q为真命题，P∧Q为假命题，故PQ一真一假，（2分）
故a≤2或3≤a≤4（4分）
点评：求已知复合命题的真假求参数的范围，应该先求出简单命题为真对应的参数范围，然后将复合命题的真假问题转化为简单命题的真假问题解决．
练习册系列答案
相关题目
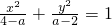表示焦点在x轴上的椭圆；如果P∨Q为真命题，P∧Q为假命题，求实数a的取值范围．
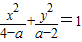表示焦点在x轴上的椭圆；如果P∨Q为真命题，P∧Q为假命题，求实数a的取值范围．