Question

如图，四面体PABC的六条棱均相等，D、E、F分别是AB、BC、CA的中点，则下列四个结论中不成立的是（　　）

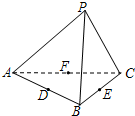
A．平面PDE⊥平面ABC	B．DF⊥平面PAE
C．BC∥平面PDF	D．平面PAE⊥平面ABC

Answer 1

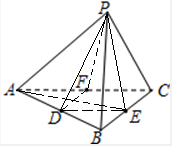
对于A，若平面PDE⊥平面ABC，因为等边△PAB中，PD⊥AB，
平面PDE∩平面ABC=AB，所以PD⊥平面ABC，可得PD⊥DE
同理可得PE⊥平面ABC，可得PE⊥DE．这样在△PDE中有两个角等于90°，
与三角形内角和定理矛盾，故平面PDE⊥平面ABC是错误的，得A不正确；
对于B，因为正△ABC中，中线AE⊥BC，同理PE⊥BC，结合线面垂直的判定定理，
得BC⊥平面PAE，又因为△ABC的中位线DF∥BC，所以DF⊥平面PAE，故B正确；
对于C，因为DF∥BC，DF?平面PDF，BC?平面PDF，故BC∥平面PDF，得C正确；
对于D，根据B项的证明得BC⊥平面PAE，结合BC?平面ABC，可得平面PAE⊥平面ABC，故D正确．
故选：A