题目内容
已知函数![]() 为常数)是实数集
为常数)是实数集![]() 上的奇函数,函数
上的奇函数,函数![]() ,使
,使![]() 在区间
在区间![]() 上是减函数的
上是减函数的![]() 的取值的集合为
的取值的集合为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ) 对![]()
![]() 及
及![]()
![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(Ⅲ)若关于![]() 的方程
的方程![]() 有且只有一个实数根,求
有且只有一个实数根,求![]() 的值.
的值.
解:(Ⅰ)![]() 是实数集
是实数集![]() 上奇函数,
上奇函数,
![]() ,即
,即![]() .
.
将![]() 带入
带入![]() ,显然为奇函数 …………………………………3分
,显然为奇函数 …………………………………3分
(Ⅱ)由(Ⅰ)知![]() ,
,![]()
![]() 要使
要使![]() 是区间
是区间![]() 上的减函数,则有
上的减函数,则有![]() 在
在![]() 恒成立,
恒成立,![]() ,所以
,所以![]() ………………………………5分
………………………………5分
要使![]() 在
在![]() 上恒成立,
上恒成立,
只需![]() 在
在![]() 时恒成立即可.
时恒成立即可.
![]() (其中
(其中![]() )恒成立即可
)恒成立即可
令![]() ,则
,则![]() 即
即![]()
![]() ,所以实数的最大值为
,所以实数的最大值为![]() ………………………………8分
………………………………8分
(Ⅲ)由(Ⅰ)知方程![]() ,即
,即![]() ,
,
令![]() ,
,![]()
当![]() 时,
时,![]() 在
在![]() 上为增函数;
上为增函数;
当![]() 时,
时,![]() 在
在![]() 上为减函数;
上为减函数;
当![]() 时,
时,![]() ……………………………………………………11分
……………………………………………………11分
而![]()
当![]() 时
时![]() 是减函数,当
是减函数,当![]() 时,
时,![]() 是增函数,
是增函数,
![]() 当
当![]() 时,
时,![]() ……………………………………………13分
……………………………………………13分
只有当![]() ,即
,即![]() 时,方程有且只有一个实数根。 ……………14分
时,方程有且只有一个实数根。 ……………14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (
( 为实常数).
为实常数).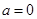 时,求
时,求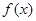 的最小值;
的最小值;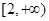 上是单调函数,求
上是单调函数,求 (
( 为实常数).
为实常数).  ,求
,求 的单调区间;
的单调区间;  ,设
,设 的最小值为
的最小值为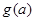 ,求
,求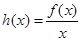 ,若函数
,若函数 在区间
在区间