题目内容
下列命题:①在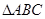 中,若
中,若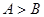 ,则
,则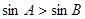 ;②已知
;②已知 ,则
,则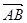 在
在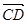 上的投影为
上的投影为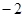 ;③已知
;③已知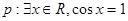 ,
,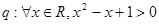 ,则“
,则“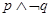 ”为假命题.其中真命题的个数为( )
”为假命题.其中真命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
C
解析试题分析:因为三角形中,A+B<π,所以若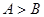 ,则
,则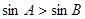 ,①是真命题;
,①是真命题;
由向量的投影的定义及夹角公式得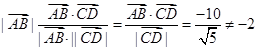 ,所以②是假命题;
,所以②是假命题;
因为p,q是真命题,所以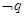 是假命题,从而
是假命题,从而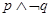 是假命题,即③是真命题,故选C。
是假命题,即③是真命题,故选C。
考点:本题主要考查命题的概念及真假判断。
点评:小综合题,涉及命题的真假判断,往往因命题涉及知识面较广,而综合性较强,就本题而言,主要涉及三角形、平面向量坐标运算、不等式等。

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
向量 在向量
在向量 上的投影是( )
上的投影是( )
A. | B. | C. | D. |
平面向量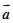 、
、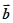 的夹角为
的夹角为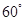 ,
,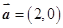 ,
,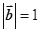 , 则
, 则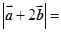 ( )
( )
A.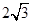 | B.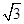 | C.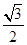 | D. |
已知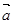 与
与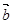 的夹角为
的夹角为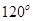 ,
,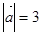 ,
,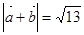 ,则
,则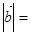 ( )
( )
| A.5 | B.4 | C.3 | D.1 |
非零向量 使得
使得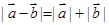 成立的一个充分非必要条件是( )
成立的一个充分非必要条件是( )
A.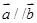 | B.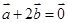 | C.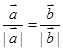 | D.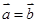 |
已知向量 ,且
,且 ,则
,则 的取值范围是( )
的取值范围是( )
A.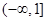 | B. | C. | D. |
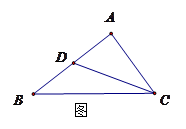
如图1所示, 是
是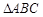 的边
的边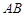 上的中点,则向量
上的中点,则向量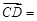 ( )
( )
A.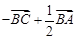 | B.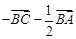 |
C.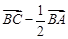 | D. |
非零向量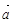 ,
,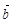 的夹角为
的夹角为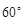 ,且
,且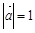 ,则
,则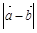 的最小值为
的最小值为
A.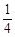 | B.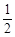 | C.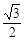 | D.1 |
 的两条直角边
的两条直角边
 两点分别在
两点分别在 轴、
轴、 轴的正半轴(含原点)上滑动,
轴的正半轴(含原点)上滑动, 分别为
分别为 的中点.则
的中点.则 的最大值是
的最大值是


