题目内容
设复数z=（1-3i）（2+i）（其中i是虚数单位），则复数z在复平面上所对应的点位于（ ）A．第一象限
B．第二象限
C．第三象限
D．第四象限
【答案】分析：利用复数的代数形式的乘除运算，得到z=（1-3i）（2+i）=5-5i．由此能求出复数z在复平面上所对应的点所在象限．
解答：解：z=（1-3i）（2+i）
=2-6i+i-3i2
=5-5i．
∴复数z在复平面上所对应的点（5，-5）位于第四象限．
故选D．
点评：本题考查复数的代数形式的乘除运算，是基础题，解题时要认真审题，仔细解答．
解答：解：z=（1-3i）（2+i）
=2-6i+i-3i2
=5-5i．
∴复数z在复平面上所对应的点（5，-5）位于第四象限．
故选D．
点评：本题考查复数的代数形式的乘除运算，是基础题，解题时要认真审题，仔细解答．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
i，则z2－2z＝
则Z2－2Z等于
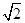i，则z2－2z等于( )