题目内容
设S、V分别表示面积和体积，如△ABC面积用S△ABC表示，三棱锥O-ABCV的体积用VO-ABC表示．对于命题：如果O是线段AB上一点，则|
|•
+|
|•
=
．将它类比到平面的情形是：若O是△ABC内一点，有S△OBC•
+S△OCA•
+S△OBA•
=
．将它类比到空间的情形应该是：若O是三棱锥A-BCD内一点，则有
| OB |
| OA |
| OA |
| OB |
| 0 |
| OA |
| OB |
| OC |
| 0 |
VO-BCD•
+VO-ACD•
+VO-ABD•
+VO-ABC•
=
| OA |
| OB |
| OC |
| OD |
| 0 |
VO-BCD•
+VO-ACD•
+VO-ABD•
+VO-ABC•
=
．| OA |
| OB |
| OC |
| OD |
| 0 |
分析：由平面图形的性质类比猜想空间几何体的性质，一般的思路是：点到线，线到面，或是二维变三维；由题目中点O在三角形ABC内，则有结论S△OBC•
+S△OAC•
+S△OAB•
=
，的结论是二维线段长与向量的关系式，类比后的结论应该为三维的体积与向量的关系式．
| OA |
| OB |
| OC |
| 0 |
解答：解：由平面图形的性质类比猜想空间几何体的性质，
一般的思路是：点到线，线到面，或是二维变三维，面积变体积；
由题目中点O在三角形ABC内，则有结论S△OBC•
+S△OAC•
+S△OAB•
=
，
我们可以推断VO-BCD•
+VO-ACD•
+VO-ABD•
+VO-ABC•
=
故答案为：VO-BCD•
+VO-ACD•
+VO-ABD•
+VO-ABC•
=
一般的思路是：点到线，线到面，或是二维变三维，面积变体积；
由题目中点O在三角形ABC内，则有结论S△OBC•
| OA |
| OB |
| OC |
| 0 |
我们可以推断VO-BCD•
| OA |
| OB |
| OC |
| OD |
| 0 |
故答案为：VO-BCD•
| OA |
| OB |
| OC |
| OD |
| 0 |
点评：本题考察的知识点是类比推理，类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．
练习册系列答案
相关题目
分别表示｜GE｜、｜EH｜的长
|·
＋|
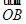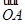.将它类比到平面的情形是：若O是△ABC内一点，有S△OBC·
＝