题目内容
 已知四边形
已知四边形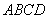 是边长为
是边长为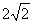 的正方形,
的正方形,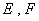 分别为
分别为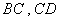 的中点,沿
的中点,沿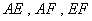 将
将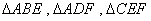 向同侧折叠且与平面
向同侧折叠且与平面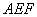 成直二面角,连接
成直二面角,连接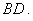
(1)求证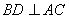 ;
;
(2)求平面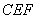 与平面
与平面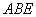 所成锐角的余弦值。
所成锐角的余弦值。
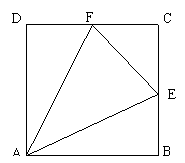
【答案】
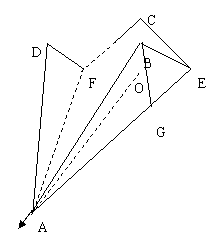
 解:(1)方法一:以EF的中点O为原点,OA为
解:(1)方法一:以EF的中点O为原点,OA为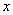 轴,OE为
轴,OE为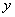 轴,OC为
轴,OC为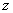 轴建立直角坐标系,则C(0 ,0 ,1),A(3 ,0 ,0),E(0 ,1 ,0),解正方形可得
轴建立直角坐标系,则C(0 ,0 ,1),A(3 ,0 ,0),E(0 ,1 ,0),解正方形可得
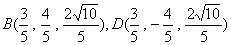
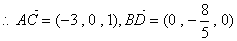
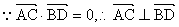
……………………………………………………………………………… 6分
(2)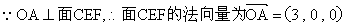
设面ABE的法向量为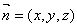
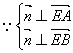 ,得
,得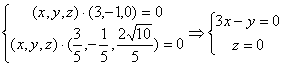
令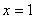 ,得一个法向量为
,得一个法向量为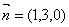 ,设锐二面角为
,设锐二面角为
则 …………………………………… 12分
…………………………………… 12分
方法二(1)过D作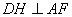 于H,过B作
于H,过B作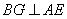 于G.
于G.

取EF中点为O,连CO、AO
则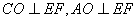 ,
,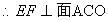
又GH//EF,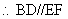 ,
,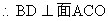 ,
,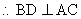 ……………………………………………………………… 6分
……………………………………………………………… 6分
 ……………… 12分
……………… 12分

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 是边长为
是边长为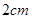 的正方形,则这个四面体的主视图的面积为________
的正方形,则这个四面体的主视图的面积为________ .
.
 是边长为
是边长为 的正方形,则这个四面体的主视图的面积为________
的正方形,则这个四面体的主视图的面积为________ .
.
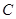 :
: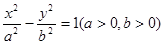 的右焦点为
的右焦点为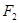 ,
,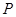 、
、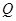 ,
, 是坐标原点,且四边形
是坐标原点,且四边形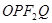 是边长为
是边长为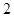 的正方形.
的正方形.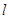 交
交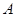 、
、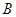 两点,线段
两点,线段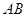 的中点为
的中点为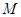 ,问
,问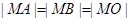 是否能成立?若成立,求直线
是否能成立?若成立,求直线 上竖一块长方形液晶广告屏幕
上竖一块长方形液晶广告屏幕 ,宣传该城市未来十年计划、目标等相关政策.已知四边形
,宣传该城市未来十年计划、目标等相关政策.已知四边形 处,点
处,点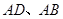 的距离分别为9米,3米,且
的距离分别为9米,3米,且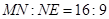 ,线段
,线段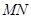 必过点
必过点 分别在边
分别在边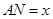 米,液晶广告屏幕
米,液晶广告屏幕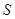 平方米.
平方米.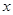 的函数关系式及其定义域;
的函数关系式及其定义域;