题目内容
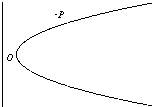
 如图,弯曲的河流是近似的抛物线C,公路l恰好是C的准线,C上的点O到l的距离最近,且为0.4千米,城镇P位于点O的北偏东30°处,|OP|=10千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路l,以便建立水陆交通网.
如图,弯曲的河流是近似的抛物线C,公路l恰好是C的准线,C上的点O到l的距离最近,且为0.4千米,城镇P位于点O的北偏东30°处,|OP|=10千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路l,以便建立水陆交通网.(1)建立适当的坐标系,求抛物线C的方程;
(2)为了降低修路成本,必须使修建的两条公路总长最小,请给出修建方案(作出图形,在图中标出此时码头Q的位置),并求公路总长的最小值(精确到0.001千米)
分析:先建立坐标系,求出抛物线方程,利用抛物线的定义知,公路总长QF+QP≥PF,从而使问题得解.
解答:解:(1)过点O作准线的垂线,垂足为A,以OA所在直线为x轴,OA的垂直平分线为y轴,建立平面直角坐标系…(2分)
由题意得,
=0.4…(4分)
所以,抛物线C:y2=1.6x…(6分)
(2)设抛物线C的焦点为F由题意得,P(5,5
)…(8分)
根据抛物线的定义知,公路总长=|QF|+|QP|≥|PF|≈9.806…(12分)
当Q为线段PF与抛物线C的交点时,公路总长最小,
最小值为9.806千米…(16分)
由题意得,
| p |
| 2 |
所以,抛物线C:y2=1.6x…(6分)
(2)设抛物线C的焦点为F由题意得,P(5,5
| 3 |
根据抛物线的定义知,公路总长=|QF|+|QP|≥|PF|≈9.806…(12分)
当Q为线段PF与抛物线C的交点时,公路总长最小,
最小值为9.806千米…(16分)
点评:本题以实际问题为载体,主要考查抛物线的标准方程及运用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
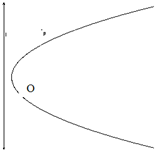 如图,弯曲的河流是近似的抛物线C,公路l恰好是C的准线,C上的点O到l的距离最近,且为0.4千米,城镇P位于点O的北偏东30°处,|OP|=10千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路l,以便建立水陆交通网.为了降低修路成本,必须使修建的两条公路总长最小,请给出修建方案.(作出图形),并求公路总长的最小值(精确到0.001千米)
如图,弯曲的河流是近似的抛物线C,公路l恰好是C的准线,C上的点O到l的距离最近,且为0.4千米,城镇P位于点O的北偏东30°处,|OP|=10千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路l,以便建立水陆交通网.为了降低修路成本,必须使修建的两条公路总长最小,请给出修建方案.(作出图形),并求公路总长的最小值(精确到0.001千米)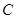 ,公路
,公路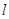 恰好是
恰好是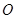 到
到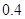 千米,城镇
千米,城镇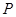 位于点
位于点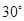 处,
处,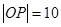 千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路
千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路 以便建立水陆交通网.
以便建立水陆交通网. 的位置),并求公路总长的最小值(精确到0.001千米)
的位置),并求公路总长的最小值(精确到0.001千米)
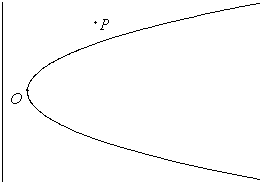 如图,弯曲的河流是近似的抛物线C,公路l恰好是C的准线,C上的点O到l的距离最近,且为0.4千米,城镇P位于点O的北偏东30°处,|OP|=10千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路l,以便建立水陆交通网.
如图,弯曲的河流是近似的抛物线C,公路l恰好是C的准线,C上的点O到l的距离最近,且为0.4千米,城镇P位于点O的北偏东30°处,|OP|=10千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路l,以便建立水陆交通网.