题目内容
设集合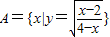 ,B={x|g(x)=lg(4x-x2)}.
,B={x|g(x)=lg(4x-x2)}.(1)集合C=
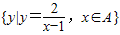 ,若a∈B,且a∉C,试求实数a的取值范围;
,若a∈B,且a∉C,试求实数a的取值范围;(2)若命题P:m∈A,命题Q:m∈B,且“P且Q”为假,“P或Q”为真,试求实数m的取值范围.
【答案】分析:(1)由题意可得A=[2,4),B=(0,4),从而可得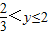 可求
可求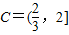 ,由a∈B,且a∉C可求a的范围
,由a∈B,且a∉C可求a的范围
(2)由题意可得P:2≤m<4,命题Q:0<m<4,由“P且Q”为假,“P或Q”为真,则P,Q中一真一假,分别求解m的范围,即可
解答:解:(1)由题意可得A={x|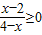 }=[2,4),B={x|4x-x2>0}=(0,4)
}=[2,4),B={x|4x-x2>0}=(0,4)
当2≤x<4时,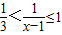 ,从而可得
,从而可得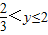
∴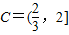 …(3分)
…(3分)
∵a∈B,且a∉C
∴a∈(0,4)且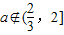
∴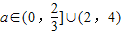 …(6分)
…(6分)
(2)由题意可得P:2≤m<4,命题Q:0<m<4
“P且Q”为假,“P或Q”为真,则P,Q中一真一假…(7分)
①若P真Q一假则有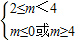 解得:m∈ϕ…(9分)
解得:m∈ϕ…(9分)
②若P真Q一假则有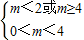 解得:0<m<2…(11分)
解得:0<m<2…(11分)
综上所述m的取值范围为(0,2)…(12分)
点评:本题主要考查了含有根式及对数函数的定义域、值域的求解,P且Q,P或Q的复合命题的真假判断的应用,属于函数知识的简单应用
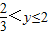 可求
可求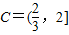 ,由a∈B,且a∉C可求a的范围
,由a∈B,且a∉C可求a的范围(2)由题意可得P:2≤m<4,命题Q:0<m<4,由“P且Q”为假,“P或Q”为真,则P,Q中一真一假,分别求解m的范围,即可
解答:解:(1)由题意可得A={x|
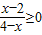 }=[2,4),B={x|4x-x2>0}=(0,4)
}=[2,4),B={x|4x-x2>0}=(0,4)当2≤x<4时,
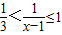 ,从而可得
,从而可得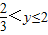
∴
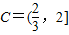 …(3分)
…(3分)∵a∈B,且a∉C
∴a∈(0,4)且
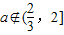
∴
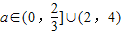 …(6分)
…(6分)(2)由题意可得P:2≤m<4,命题Q:0<m<4
“P且Q”为假,“P或Q”为真,则P,Q中一真一假…(7分)
①若P真Q一假则有
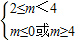 解得:m∈ϕ…(9分)
解得:m∈ϕ…(9分)②若P真Q一假则有
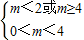 解得:0<m<2…(11分)
解得:0<m<2…(11分)综上所述m的取值范围为(0,2)…(12分)
点评:本题主要考查了含有根式及对数函数的定义域、值域的求解,P且Q,P或Q的复合命题的真假判断的应用,属于函数知识的简单应用

练习册系列答案
相关题目

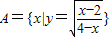 ,B={x|g(x)=lg(4x-x2)}.
,B={x|g(x)=lg(4x-x2)}.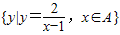 ,若a∈B,且a∉C,试求实数a的取值范围;
,若a∈B,且a∉C,试求实数a的取值范围;