题目内容
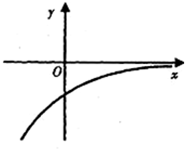已知函数 f（x）的定义域为R，其导函数f′（x）的图象如图所示，则对于任意x1，x2∈R（ x1≠x2），下列结论正确的是
①f（x）＜0恒成立；
②（x1-x2）[f（x1）-f（x2）]＜0；
③（x1-x2）[f（x1）-f（x2）]＞0；
④
；
⑤
．
- A.①③
- B.①③④
- C.②④
- D.②⑤
D
分析：由导函数的图象可知，导函数f′（x）的图象在x轴下方，即f′（x）＜0，故原函数为减函数，并且是，递减的速度是先快后慢．由此可得函数f（x）的图象，再结合函数图象易得正确答案．
解答：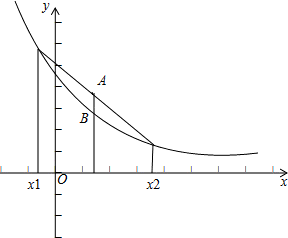
解：由导函数的图象可知，导函数f′（x）的图象在x轴下方，即f′（x）＜0，故原函数为减函数，
并且是，递减的速度是先快后慢．所以f（x）的图象如图所示．
f（x）＜0恒成立，没有依据，故①不正确；
②表示（x1-x2）与[f（x1）-f（x2）]异号，即f（x）为减函数．故②正确；
③表示（x1-x2）与[f（x1）-f（x2）]同号，即f（x）为增函数．故③不正确，
④⑤左边边的式子意义为x1，x2中点对应的函数值，即图中点B的纵坐标值，
右边式子代表的是函数值得平均值，即图中点A的纵坐标值，显然有左边小于右边，
故④不正确，⑤正确，综上，正确的结论为②⑤．
故选D．
点评：本题为导函数的应用，由导函数的图象推出原函数应具备的性质，利用数形结合是解决问题的关键，属基础题．
分析：由导函数的图象可知，导函数f′（x）的图象在x轴下方，即f′（x）＜0，故原函数为减函数，并且是，递减的速度是先快后慢．由此可得函数f（x）的图象，再结合函数图象易得正确答案．
解答：
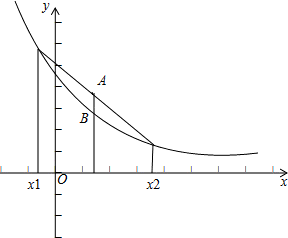解：由导函数的图象可知，导函数f′（x）的图象在x轴下方，即f′（x）＜0，故原函数为减函数，并且是，递减的速度是先快后慢．所以f（x）的图象如图所示．
f（x）＜0恒成立，没有依据，故①不正确；
②表示（x1-x2）与[f（x1）-f（x2）]异号，即f（x）为减函数．故②正确；
③表示（x1-x2）与[f（x1）-f（x2）]同号，即f（x）为增函数．故③不正确，
④⑤左边边的式子意义为x1，x2中点对应的函数值，即图中点B的纵坐标值，
右边式子代表的是函数值得平均值，即图中点A的纵坐标值，显然有左边小于右边，
故④不正确，⑤正确，综上，正确的结论为②⑤．
故选D．
点评：本题为导函数的应用，由导函数的图象推出原函数应具备的性质，利用数形结合是解决问题的关键，属基础题．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
已知函数f（x）的定义域为[-1，5]，部分对应值如下表．
已知函数f（x）的部分图象如图所示，则f（x）的解析式可能为（ ）
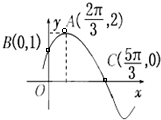
A、f（x）=2sin（
| ||||
B、f（x）=
| ||||
C、f（x）=2sin（
| ||||
D、f（x）=
|
已知函数f（x）的定义域为[-3，+∞），部分函数值如表所示，其导函数的图象如图所示，若正数a，b满足f（2a+b）＜1，则